题目内容
函数 的单调递增区间是 .
的单调递增区间是 .
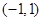 (-1可以取等号,1不可以)
(-1可以取等号,1不可以)
解析试题分析:由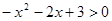 ,得
,得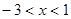 ;又函数
;又函数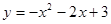 在区间
在区间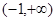 上是减函数,利用复合函数单调性的判定得,函数的单调递增区间是(-1,1).
上是减函数,利用复合函数单调性的判定得,函数的单调递增区间是(-1,1).
考点:复合函数单调性的判定

练习册系列答案
相关题目
题目内容
函数 的单调递增区间是 .
的单调递增区间是 .
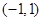 (-1可以取等号,1不可以)
(-1可以取等号,1不可以)
解析试题分析:由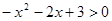 ,得
,得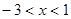 ;又函数
;又函数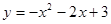 在区间
在区间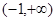 上是减函数,利用复合函数单调性的判定得,函数的单调递增区间是(-1,1).
上是减函数,利用复合函数单调性的判定得,函数的单调递增区间是(-1,1).
考点:复合函数单调性的判定
