题目内容
定义域为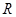 的奇函数
的奇函数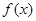 满足
满足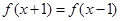 ,且当
,且当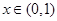 时,
时, 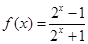 .
.
(Ⅰ)求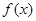 在
在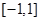 上的解析式;
上的解析式;
(Ⅱ)当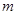 取何值时,方程
取何值时,方程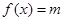 在
在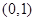 上有解?
上有解?
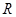 的奇函数
的奇函数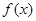 满足
满足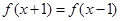 ,且当
,且当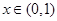 时,
时, 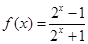 .
.(Ⅰ)求
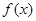 在
在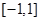 上的解析式;
上的解析式;(Ⅱ)当
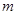 取何值时,方程
取何值时,方程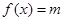 在
在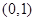 上有解?
上有解?(Ⅰ)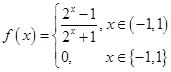 ;(Ⅱ)
;(Ⅱ)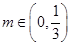 .
.
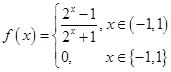 ;(Ⅱ)
;(Ⅱ)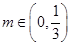 .
.试题分析:(Ⅰ)先设自变量
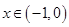 ,先求出
,先求出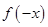 的表达式,然后根据奇函数的定义
的表达式,然后根据奇函数的定义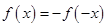 即可求出函数
即可求出函数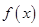 在
在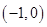 上的解析式,对于其它点出的函数值,则根据其它条件确定;(Ⅱ)把问题进行适当转化,方程
上的解析式,对于其它点出的函数值,则根据其它条件确定;(Ⅱ)把问题进行适当转化,方程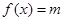 在
在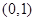 上有解
上有解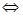
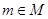 (其中
(其中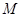 为函数
为函数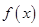 在
在 上的值域),只需根据不等式的性质或函数的单调性确定函数
上的值域),只需根据不等式的性质或函数的单调性确定函数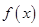 在
在 上的值域就可以确定实数
上的值域就可以确定实数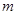 的取值范围了.
的取值范围了.试题解析:(Ⅰ)当
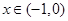 时,
时,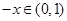 ,由
,由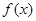 为
为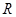 上的奇函数,
上的奇函数,得
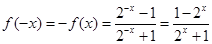 ,
,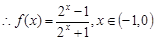 ,又有奇函数得
,又有奇函数得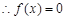
又
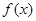 满足
满足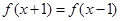
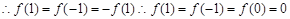
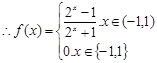 5分
5分(Ⅱ)当
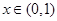
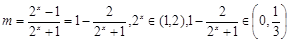 即
即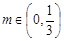 10分
10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
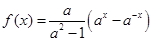 ,其中
,其中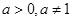
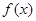 ,当
,当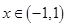 时,
时,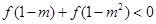 ,求实数
,求实数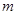 的取值集合;
的取值集合;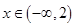 时,
时,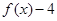 的值为负,求
的值为负,求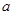 的取值范围.
的取值范围.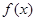 是定义在
是定义在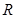 上的奇函数,当
上的奇函数,当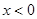 时,
时,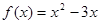 ,则当
,则当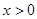 时,
时, 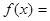
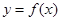 满足条件
满足条件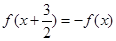 ,且
,且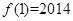 ,则
,则 .
.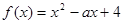 ,若
,若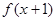 是偶函数,则实数
是偶函数,则实数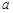 的值为( )
的值为( )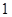
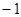
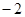
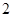
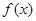 的定义域为
的定义域为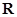 ,周期为2,且当
,周期为2,且当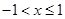 时,
时,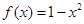 .若直线
.若直线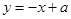 与曲线
与曲线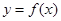 恰有2个交点,则实数
恰有2个交点,则实数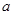 的所有可能取值构成的集合为( )
的所有可能取值构成的集合为( )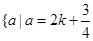 或
或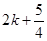
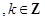
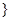
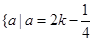 或
或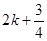
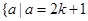 或
或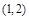 内是增函数的为( )
内是增函数的为( )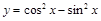
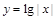
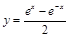
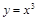
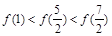
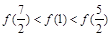
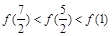
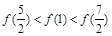
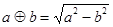 ,
,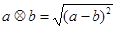 ,则函数
,则函数 为( )
为( )