题目内容
（2007•温州一模）已知f(x)=
+2sinxcosx-2
sin2x，
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）写出函数f（x）的单调减区间．
| 3 |
| 3 |
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）写出函数f（x）的单调减区间．
分析：（Ⅰ）先用降幂公式和辅助角公式，将f（x）进行整理，得f（x）=2sin(2x+
)，然后根据正弦函数周期的公式可得函数f（x）的最小正周期为π；
（Ⅱ）根据正弦函数的单调性，将2x+
当成一个整体，解不等式
+2kπ≤2x+
≤
+2kπ，k∈Z，得到的x的解集，写成区间就是函数f（x）的单调减区间．
| π |
| 3 |
（Ⅱ）根据正弦函数的单调性，将2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答：解：（Ⅰ）f(x)=
+2sinxcosx-2
sin2x=
+sin2x-
(1-cos2x)
=sin2x+
cos2x=2sin(2x+
)…（5分）
∴f（x）的最小正周期为
=π …（7分）
（Ⅱ）由
+2kπ≤2x+
≤
+2kπ，k∈Z …．（10分）
得
+kπ≤x≤
+kπ，k∈Z
则函数f（x）的单调减区间为[
+kπ，
+kπ]，k∈Z…（14分）
| 3 |
| 3 |
| 3 |
| 3 |
=sin2x+
| 3 |
| π |
| 3 |
∴f（x）的最小正周期为
| 2π |
| 2 |
（Ⅱ）由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
得
| π |
| 12 |
| 7π |
| 12 |
则函数f（x）的单调减区间为[
| π |
| 12 |
| 7π |
| 12 |
点评：本题考查了三角函数中的恒等变换应用，着重考查了辅助角公式，三角函数的图象与性质等知识点，属于中档题．
练习册系列答案
相关题目
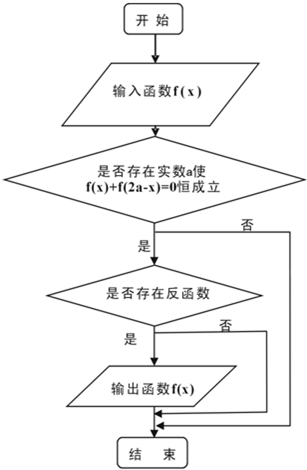（2007•温州一模）某流程如图所示，现输入如下四个函数，则可以输出的函数是（ ）