题目内容
已知椭圆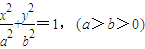 左、右焦点分别为F1(-c,0),F2(c,0),点A、B坐标为A(a,0),B(0,b),若△ABC面积为
左、右焦点分别为F1(-c,0),F2(c,0),点A、B坐标为A(a,0),B(0,b),若△ABC面积为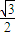 ,∠BF2A=120°.
,∠BF2A=120°.(1)求椭圆的标准方程;
(2)若直线y=kx+2与椭圆交于不同的两点M、N,且以MN为直径的圆恰好过原点,求实数k的取值;
(3)动点P使得
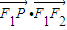 、
、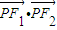 、
、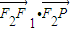 成公差小于零的等差数列,记θ为向量
成公差小于零的等差数列,记θ为向量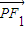 与
与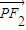 的夹角,求θ的取值范围.
的夹角,求θ的取值范围.
【答案】分析:(1)在RT△BOF2中,∠BF2O=60°,计算得: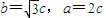 ,由
,由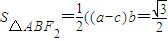 ,可计算得
,可计算得 ,从而可求椭圆标准方程.
,从而可求椭圆标准方程.
(2)设直线l的方程为y=kx+2.与椭圆方程联立,根据判别式大于0求得k的范围,设M,N两点坐标分别为M(x1,y1),N(x2,y2).根据韦达定理求得x1+x2和x1x2,进而根据若以MN为直径的圆恰好过原点,x1•x2+y1•y2=0,代入即可求得k,最后检验看是否符合题意.
(3)设P的坐标,由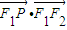 、
、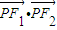 、
、 成公差小于零的等差数列得:x2+y2=33≥x2>0
成公差小于零的等差数列得:x2+y2=33≥x2>0
从而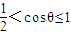 ,所以可求θ的取值范围..
,所以可求θ的取值范围..
解答:解:(1)在RT△BOF2中,∠BF2O=60°,计算得: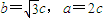
由 ,计算得
,计算得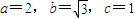 ,所以椭圆标准方程为
,所以椭圆标准方程为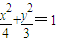 .
.
(2)设交点M、N坐标为M(x1,y1),N(x2,y2)
将直线y=kx+2代入椭圆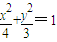 整理得方程,3+4k2)x2+16kx+4=0;
整理得方程,3+4k2)x2+16kx+4=0;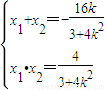
由△>0得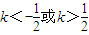
由MN为直径的圆过原点得x1•x2+y1•y2=0,所以x1•x2+(kx1+2)(kx2+2)=0,计算并检验得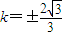 即为所求.
即为所求.
(3)设P(x,y),由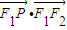 、
、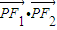 、
、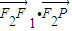 成公差小于零的等差数列得:x2+y2=33≥x2>0
成公差小于零的等差数列得:x2+y2=33≥x2>0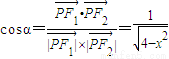
所以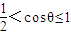 ,所以
,所以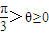 .
.
点评:本题主要考查椭圆标准方程的求解,考查直线与椭圆的位置关系,考查学生分析解决问题的能力.
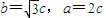 ,由
,由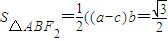 ,可计算得
,可计算得 ,从而可求椭圆标准方程.
,从而可求椭圆标准方程.(2)设直线l的方程为y=kx+2.与椭圆方程联立,根据判别式大于0求得k的范围,设M,N两点坐标分别为M(x1,y1),N(x2,y2).根据韦达定理求得x1+x2和x1x2,进而根据若以MN为直径的圆恰好过原点,x1•x2+y1•y2=0,代入即可求得k,最后检验看是否符合题意.
(3)设P的坐标,由
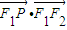 、
、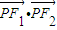 、
、 成公差小于零的等差数列得:x2+y2=33≥x2>0
成公差小于零的等差数列得:x2+y2=33≥x2>0从而
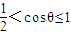 ,所以可求θ的取值范围..
,所以可求θ的取值范围..解答:解:(1)在RT△BOF2中,∠BF2O=60°,计算得:
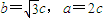
由
 ,计算得
,计算得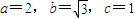 ,所以椭圆标准方程为
,所以椭圆标准方程为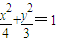 .
.(2)设交点M、N坐标为M(x1,y1),N(x2,y2)
将直线y=kx+2代入椭圆
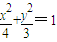 整理得方程,3+4k2)x2+16kx+4=0;
整理得方程,3+4k2)x2+16kx+4=0;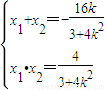
由△>0得
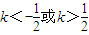
由MN为直径的圆过原点得x1•x2+y1•y2=0,所以x1•x2+(kx1+2)(kx2+2)=0,计算并检验得
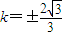 即为所求.
即为所求.(3)设P(x,y),由
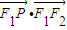 、
、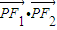 、
、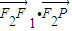 成公差小于零的等差数列得:x2+y2=33≥x2>0
成公差小于零的等差数列得:x2+y2=33≥x2>0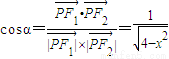
所以
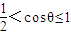 ,所以
,所以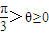 .
.点评:本题主要考查椭圆标准方程的求解,考查直线与椭圆的位置关系,考查学生分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•茂名二模)已知椭圆
(2012•茂名二模)已知椭圆 左、右焦点分别为F1、F2,点
左、右焦点分别为F1、F2,点 ,点F2在线段PF1的中垂线上。
,点F2在线段PF1的中垂线上。 与椭圆C交于M、N两点,直线F2M与F2N的倾斜角互补,求证:直线
与椭圆C交于M、N两点,直线F2M与F2N的倾斜角互补,求证:直线 过定点,并求该定点的坐标。
过定点,并求该定点的坐标。