题目内容
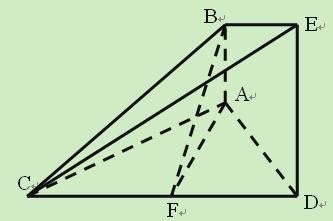
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.
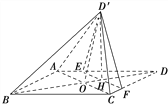
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱锥D′ABCFE的体积.
,求五棱锥D′ABCFE的体积.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)折叠后仍有EF⊥HD,而AC∥EF,可得AC⊥HD′.(2)先定高线:OD′,由勾股定理得OD′⊥OH.由(1)得AC⊥OD′.因此OD′⊥平面ABC.再根据锥体体积公式求体积
试题解析:(1)证明:由已知得AC⊥BD,AD=CD.
又由AE=CF得![]() =
=![]() ,故AC∥EF.
,故AC∥EF.
由此得EF⊥HD,故EF⊥HD′,所以AC⊥HD′.
(2)由EF∥AC得![]() .
.
由AB=5,AC=6得DO=BO=![]() =4.
=4.
所以OH=1,D′H=DH=3.
于是OD′2+OH2=(2![]() )2+12=9=D′H2,
)2+12=9=D′H2,
故OD′⊥OH.
由(1)知AC⊥HD′,又AC⊥BD,BD∩HD′=H,
所以AC⊥平面BHD′,于是AC⊥OD′.
又由OD′⊥OH,AC∩OH=O,所以OD′⊥平面ABC.
又由![]() =
=![]() 得EF=
得EF=![]() .
.
五边形ABCFE的面积S=![]() ×6×8-
×6×8-![]() ×
×![]() ×3=
×3=![]() .
.
所以五棱锥D′ABCFE的体积V=![]() ×
×![]() ×2
×2![]() =
=![]() .
.
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目