Question

（本小题满分12分）

已知不等式为大于2的整数，表示不超过的最大整数. 设数列的各项为正，且满足

   （Ⅰ）证明

（Ⅱ）猜测数列是否有极限？如果有，写出极限的值（不必证明）；

（Ⅲ）试确定一个正整数N，使得当时，对任意b>0，都有．

Answer 1

略

解析:

（Ⅰ）证法1：∵当

即  于是有 

所有不等式两边相加可得 

由已知不等式知，当n≥3时有，

∵

证法2：设，首先利用数学归纳法证不等式

   （i）当n=3时，  由 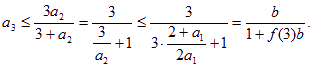  知不等式成立.

（ii）假设当n=k（k≥3）时，不等式成立，即

则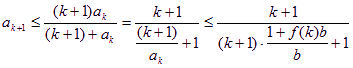

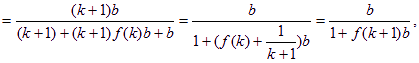
即当n=k+1时，不等式也成立.由（i）、（ii）知，

又由已知不等式得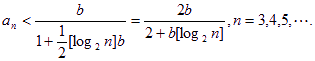 

   （Ⅱ）有极限，且

   （Ⅲ）∵则有

故取N=1024，可使当n>N时，都有