题目内容

3．函数f（x）=|logax|（0＜a＜1）的单调递增区间是（1，+∞）．

分析 根据logax的符号化简f（x）的解析式，从而得出答案．

解答 解：①当logax≥0，即0＜x≤1时，f（x）=logax，∵0＜a＜1，∴f（x）在（0，1]上是减函数；
②当logax＜0，即x＞1时，f（x）=-logax，∴f（x）在（1，+∞）上是增函数．
故答案为（1，+∞）．

点评 本题考查了绝对值的化简，对数函数的单调性，属于基础题．

练习册系列答案
相关题目
13．已知函数f（x）=$\frac{x-1}{1+x}$．
（1）求证：函数f（x）在区间（-1，+∞）上是增加的；
（2）设g（x）=f（2x），求证：函数g（x）是奇函数；
（3）在（2）的前提下，若g（x-1）+g（3-2x）＜0，求实数x的取值集合．
14．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+bx+c，（-4≤x＜0）}\\{-x+3，（x≥0）}\end{array}\right.$，若f（-4）=f（0），f（-2）=-1．
（1）求函数f（x）的解析式；
（2）画出函数f（x）的图象，并指出函数的定义域、值域、单调区间．
11．在△ABC中，若tanA=2tanB，a2-b2=$\frac{1}{3}$c，则c=1．
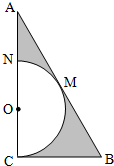18．如图，△ABC中，∠C=90°，∠A=30°，BC=1，在三角形内挖去半圆，圆心O在边AC上，半圆与BC、AB相切于点C、M，与AC交于点N，则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$．
8．已知函数f（x）=x2+（m-2）x-5-m有两个小于2的零点，则实数m的取值范围（　　）
A．（5，+∞）B．（2，+∞）C．（-∞，2）D．（2，5）
15．若关于x、y的方程（m2-4m-5）x2+（m2+5m-6）y2=1表示焦点在y轴上的双曲线，则实数m的取值范围是（1，5）．
12．在△ABC中，边a，b，c分别为角A，B，C的对边，若a=$\sqrt{3}$，∠A=$\frac{π}{3}$，则当b取最大值时，△ABC的面积为$\frac{\sqrt{3}}{2}$．
13．已知动点P在棱长为1的正方体ABCD-A1B1C1D1的表面上运动，且PA=r（0＜r＜$\sqrt{3}$），记点P的轨迹长度为f（r）．给出以下四个命题：
①f（1）=$\frac{3}{2}$π；②f（$\sqrt{2}$）=$\sqrt{3}π$；③f（$\frac{2\sqrt{3}}{3}$）=$\frac{2\sqrt{3}}{3}$π；
④函数f（r）在（0，1）上是增函数，f（r）在（$\sqrt{2}$，$\sqrt{3}$）上是减函数．其中为真命题的是（　　）
A．①③B．②③C．①④D．②④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网