题目内容
本小题满分16分)设不等式组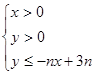 所表示的平面区域为
所表示的平面区域为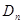 ,记
,记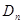 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为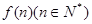
(1)求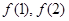 的值及
的值及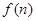 的表达式;
的表达式;
(2)记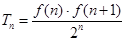 ,试比较
,试比较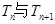 的大小;若对于一切的正整数
的大小;若对于一切的正整数 ,总有
,总有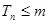 成立,求实数
成立,求实数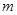 的取值范围;
的取值范围;
(3)设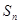 为数列
为数列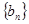 的前
的前 项的和,其中
项的和,其中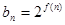 ,问是否存在正整数
,问是否存在正整数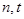 ,使
,使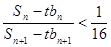 成立?若存在,求出正整数
成立?若存在,求出正整数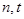 ;若不存在,说明理由.
;若不存在,说明理由.
⑴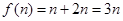
⑵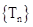 中的最大值为
中的最大值为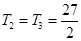
要使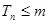 对于一切的正整数
对于一切的正整数 恒成立,只需
恒成立,只需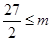 ∴
∴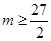
⑶存在正整数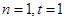 使
使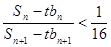 成立.
成立.
解析试题分析:(1)据可行域,求出当x=1,x=2时,可行域中的整数点,分别求出f(1),f(2),f(n).
(2)求出 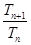 ,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
(3) 因为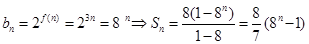 ,
,
然后可由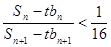 ,得,
,得,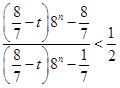 ,再分t=1和t>1两种情况进行研究即可.
,再分t=1和t>1两种情况进行研究即可.
⑴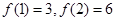
当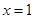 时,
时,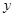 取值为1,2,3,…,
取值为1,2,3,…,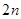 共有
共有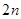 个格点
个格点
当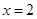 时,
时,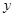 取值为1,2,3,…,
取值为1,2,3,…, 共有
共有 个格点
个格点
∴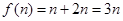
⑵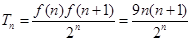
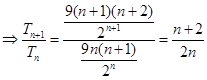
当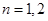 时,
时,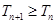
当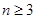 时,
时,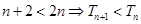
∴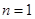 时,
时,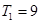
 时,
时,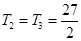
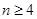 时,
时,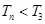
∴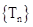 中的最大值为
中的最大值为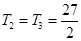
要使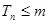 对于一切的正整数
对于一切的正整数 恒成立,只需
恒成立,只需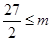 ∴
∴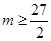
⑶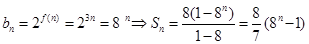
将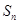 代入
代入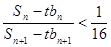 ,化简得,
,化简得,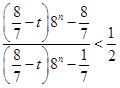 (﹡)
(﹡)
若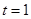 时
时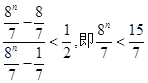 ,显然
,显然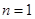
若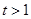 时
时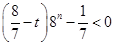 (﹡)式化简为
(﹡)式化简为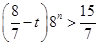 不可能成立
不可能成立
综上,存在正整数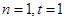 使
使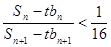 成立.
成立.
考点:二元一次不等式组表示平面区域,函数的数列特性,数列与函数的综合.
点评:解本小题的关键是正确作出可行域,然后得出f(n)=3n,这也是解决本小题的前提.
然后利用研究函数的单调性的方法研究数列的单调性,研究有关数列不等式恒成立问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知 若
若 在
在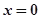 处连续,则
处连续,则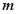 的值为( )
的值为( )
A.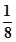 | B.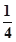 | C. | D.2 |
设 、
、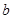 、
、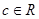 ,
,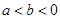 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.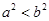 | B. | C.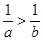 | D.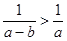 |
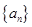 和
和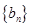 满足
满足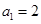 ,
,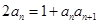 ,
,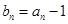 。
。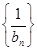 为等差数列,并求数列
为等差数列,并求数列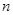 项和为
项和为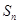 ,令
,令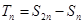 ,求
,求 的最小值。
的最小值。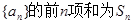 ,
,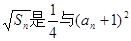 的等比中项。
的等比中项。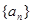 是等差数列;
是等差数列;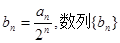 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。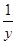 )+(x2+
)+(x2+ )+…+(xn+
)+…+(xn+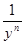 )(y
)(y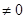 )。
)。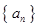 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,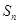 为其前n项和,且满足
为其前n项和,且满足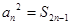 ,
,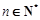 .数列
.数列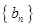 满足
满足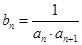 ,
, 为数列
为数列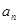 和数列
和数列 ,不等式
,不等式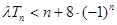 恒成立,求实数
恒成立,求实数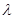 的取值范围;
的取值范围;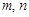
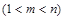 ,使得
,使得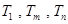 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有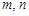 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.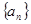 的前
的前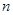 项和为
项和为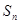 ,满足
,满足 .
. ;
;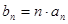 ,求数列
,求数列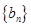 的前
的前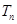 .
.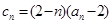 ,若对任意的正整数
,若对任意的正整数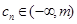 ,求实数
,求实数 的取值范围.
的取值范围.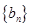 中,
中,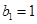 ,且点
,且点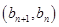 在直线
在直线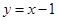 上.数列
上.数列 中,
中,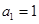 ,
, ,
, ,求数列
,求数列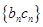 的前
的前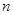 项和
项和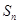 .
.