题目内容

已知曲线C：（x-1）2+y2=1，点A（-1，0）及点B（2，a），从点A观察点B，要使视线不被曲线C拦住，则a的取值范围为（　　）
分析：根据题意画出图形，如图所示，当直线AB与圆E相切时，此时B与C（或D）重合，此时圆心到直线AB的距离d=r，利用点到直线的距离公式列出关于a的方程，求出方程的解得到a的值，即可确定出满足题意a的范围．
解答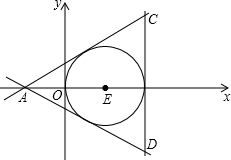：解：根据题意画出图形，当AB直线与圆E相切时，B与C（或D）重合），此时直线AB解析式为ax-3y+a=0，
∴圆心（1，0）到切线的距离d=r，即
|2a|
a2+9
=1，
解得：a=±
3
，
由图象得：要使视线不被曲线C拦住，a的取值范围为（-∞，-
3
）∪（
3
，+∞）．
故选B
点评：此题考查了直线与圆的位置关系，当直线与圆相切时，圆心到直线的距离等于圆的半径，熟练掌握此性质是解本题的关键．
练习册系列答案
相关题目
（2006•石景山区一模）如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，点N的轨迹为曲线E．
（Ⅰ） 求曲线E的方程；
（Ⅱ） 若点B1（x1，y1），B2（-1，y2），B3（x3，y3）在曲线E上，线段B1B3的垂直平分线为直线l，且|B1A|，|B2A|，|B3A|成等差数列，求x1+x3的值，并证明直线l过定点；
（Ⅲ）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足
FG
=λ
FH
，求λ的取值范围．
已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若直线y=kx+
k2+1
与（1）中所求点N的轨迹E交于不同两点F，H，O是坐标原点，且
2
3
≤
OF
•
OH
≤
3
4
，求△FOH的面积的取值范围．
已知曲线C：x2y+xy2=1，则曲线C关于对称的序号有（　　）
（1）x轴对称；（2）y轴对称；（3）原点对称；（4）直线y=x对称；（5）直线y=-x对称．
给出下列四个命题：
①如果复数z满足|z+i|+|z-i|=2，则复数z在复平面上所对应点的轨迹是椭圆．
②设f（x）是定义在R上的函数，且对任意的x∈R，|f（x）|=|f（-x）|恒成立，则f（x）是R上的奇函数或偶函数．
③已知曲线C：
x2
9
-
y2
16
=1和两定点E（-5，0）、F（5，0），若P（x，y）是C上的动点，则||PE|-|PF||＜6．
④设定义在R上的两个函数f（x）、g（x）都有最小值，且对任意的x∈R，命题“f（x）＞0或g（x）＞0”正确，则f（x）的最小值为正数或g（x）的最小值为正数．
上述命题中错误的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网