题目内容
已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
=2
,
•
=0,点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若直线y=kx+
与(1)中所求点N的轨迹E交于不同两点F,H,O是坐标原点,且
≤
•
≤
,求△FOH的面积的取值范围.
 |
| AM |
 |
| AP |
 |
| NP |
 |
| AM |
(1)求曲线E的方程;
(2)若直线y=kx+
| k2+1 |
| 2 |
| 3 |
| OF |
| OH |
| 3 |
| 4 |
分析:(1)由于AM=2AP且NP⊥AM即NP为AM的中垂线故联想到连接NA即可观察出NA+NC=CM=2
在根据圆锥曲线的定义可写出曲线E的方程.
根据题意,先证明出NP为线段AM的垂直平分线,利用垂直平分线定理得到点N到点A、C的距离和为常数,从而得出所求轨迹是以A、C为焦点的椭圆,不难求出它的方程;
(2)在(1)的基础上,将直线y=kx+
与椭圆方程联解消去y得关于x的方程,再利用根与系数的关系,得到
,将这个关系代入到数量积
•
当中,表示成关于k的式子,再进行化简,最终得到不等式
≤
≤
,解这个不等式可得k2的取值范围,将△FOH的面积用k表示,从而可求出面积的取值范围.
| 2 |
根据题意,先证明出NP为线段AM的垂直平分线,利用垂直平分线定理得到点N到点A、C的距离和为常数,从而得出所求轨迹是以A、C为焦点的椭圆,不难求出它的方程;
(2)在(1)的基础上,将直线y=kx+
| k2+1 |
|
| OF |
| OH |
| 2 |
| 3 |
| k2+1 |
| 2k 2+1 |
| 3 |
| 4 |
解答: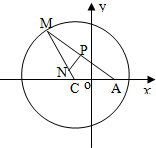 解:(1)
解:(1)
=2
,,
•
=0
所以NP为线段AM的垂直平分线,|NA|=|NM|
|NC|+|NA|=|NC|+|MN|=2
>2=|CA|
所以动点N的轨迹是以C(-1,0),A(1,0)为焦点的椭圆,
且长轴长为2a=2
,焦距2c=2,所以a=
,c=1,b2=1
曲线E的方程为
+y2=1.
(2)设F(x1,y1)H(x2,y2),则由
,消去y得
(2k2+1)x2+4k
x+2k2=0,△=8k2>0 (k≠0)
∴x1+x2=-
,x1x2=
•
=x 1x 2+y 1y 2=x 1x 2+(kx 1+
)(kx 2+
)
=(k2+1)x1x2+k
(x1+x2)+k2+1
=
-
+k2+1=
∴
≤
≤
⇒
≤k2≤1
∵|FH|=
=
又点O到直线EH的距离d=1,
∴S=
令t=2k2+1,t∈[2,3],k2=
(t-1)
∴S=
∵2≤t≤3
∴
≤
≤
∴
≤S≤
 解:(1)
解:(1) |
| AM |
. |
| AP |
 |
| NP |
. |
| AM |
所以NP为线段AM的垂直平分线,|NA|=|NM|
|NC|+|NA|=|NC|+|MN|=2
| 2 |
所以动点N的轨迹是以C(-1,0),A(1,0)为焦点的椭圆,
且长轴长为2a=2
| 2 |
| 2 |
曲线E的方程为
| x 2 |
| 2 |
(2)设F(x1,y1)H(x2,y2),则由
|
(2k2+1)x2+4k
| k2+1 |
∴x1+x2=-
4k
| ||
| 2k2+1 |
| 2k 2 |
| 2k 2+1 |
| OF |
| OH |
| k2+1 |
| k2+1 |
=(k2+1)x1x2+k
| k2+1 |
=
| (k 2+1)•2k 2 |
| 2k 2+1 |
| (k 2+1)•4k 2 |
| 2k 2+1 |
| k 2 +1 |
| 2k 2+1 |
∴
| 2 |
| 3 |
| k2+1 |
| 2k 2+1 |
| 3 |
| 4 |
| 1 |
| 2 |
∵|FH|=
| (1+k2)[(x1+x2) 2-4x1x2] |
2
| ||
| 2k2+1 |
又点O到直线EH的距离d=1,
∴S=
| ||
| 2k2+1 |
令t=2k2+1,t∈[2,3],k2=
| 1 |
| 2 |
∴S=
| ||
| 2 |
1-
|
∵2≤t≤3
∴
| 1 |
| 9 |
| 1 |
| t2 |
| 1 |
| 4 |
∴
| ||
| 4 |
| 2 |
| 3 |
点评:本题是直线与圆锥曲线的综合问题的考查,是综合题有一定的难度.主要考查了利用圆锥曲线的定义求曲线方程,考查平面向量的数量积运算,同时考查里哦啊设而不求和转化化归思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目