题目内容
对于函数y=f(x),我们把使f(x)=0的实数叫做函数y=f(x)的零点,设x是函数f(x)=x2-|log2x|的一个零点,则x所在的一个区间是( )A.
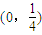
B.
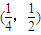
C.
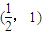
D.(1,+∞)
【答案】分析:由零点存在定理知,当在某区间两个端点处的函数值的符号相反,则在此区间必有零点,由此规则对四个选项中的区间端点的函数值的符号进行验证,即可选出正确选项
解答:解:由题意,当x的值分别取 ,
, ,1,函数值分别为-
,1,函数值分别为-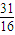 ,-
,- ,1,
,1,
所以可以确定,函数必在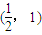 内有零点
内有零点
∴x所在的一个区间是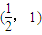
故选C
点评:本题考查对函数零点判定定理的理解,解题的关键是由零点存在定理得出某个区间是否存在零点的判断方法,零点存在定理是一个充分条件,即两端点处函数值符号相反,可得出函数在此区间内有零点,而当区间中有零点时函数在区间两端点的函数值符号不一定相反.本题考查基本概念,属于数学知识的架构题型,此考点是近几年高考中的常考内容,要注意理解掌握.
解答:解:由题意,当x的值分别取
 ,
, ,1,函数值分别为-
,1,函数值分别为-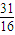 ,-
,- ,1,
,1,所以可以确定,函数必在
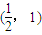 内有零点
内有零点∴x所在的一个区间是
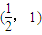
故选C
点评:本题考查对函数零点判定定理的理解,解题的关键是由零点存在定理得出某个区间是否存在零点的判断方法,零点存在定理是一个充分条件,即两端点处函数值符号相反,可得出函数在此区间内有零点,而当区间中有零点时函数在区间两端点的函数值符号不一定相反.本题考查基本概念,属于数学知识的架构题型,此考点是近几年高考中的常考内容,要注意理解掌握.

练习册系列答案
相关题目