Question

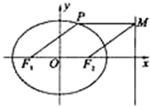如图，点P在椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)上，F₁、F₂分别是椭圆的左、右焦点，过点P作椭圆右准线的垂线，垂足为M，若四边形PF₁F₂M为菱形，则椭圆的离心率是（　　）

• A、

  2

  2

• B、

  3

  2

• C、

  3 -1

  2

• D、

  5 -1

  2

Answer 1

分析：由菱形的性质可得PM=F₁F₂=2c=PF₁，根据椭圆的第二定义可得  

PF2

PM

=e=

c

a

，解方程求得答案．

解答：解：∵四边形PF₁F₂M为菱形，∴PM=F₁F₂=2c，且 PM=PF₁=2c．
再由椭圆的定义可得 PF₁+PF₂=2a，∴PF₂=2a-2c．
根据椭圆的第二定义可得 

PF2

PM

=e=

c

a

，
∴

2a-2c

2c

=

c

a

，∴c²=a²-ac，∴e²+e-1=0，
根据0＜e＜1，解得e=

-1+ 5

2

，
故椭圆的离心率e=

-1+ 5

2

，
故选 D．

点评：本题主要考查了椭圆的定义和简单性质，求出 PF₂=2a-2c，是解题的关键．