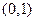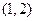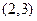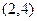题目内容
已知函数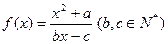 ,若方程
,若方程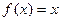 有且只有两个相异根0和2,且
有且只有两个相异根0和2,且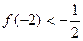 (1)求函数
(1)求函数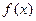 的解析式。(2)已知各项不为1的数列{an}满足
的解析式。(2)已知各项不为1的数列{an}满足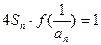 ,求数列通项an。(3)如果数列{bn}满足
,求数列通项an。(3)如果数列{bn}满足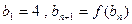 ,求证:当
,求证:当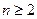 时,恒有
时,恒有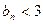 成立。
成立。
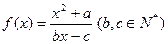 ,若方程
,若方程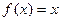 有且只有两个相异根0和2,且
有且只有两个相异根0和2,且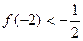 (1)求函数
(1)求函数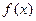 的解析式。(2)已知各项不为1的数列{an}满足
的解析式。(2)已知各项不为1的数列{an}满足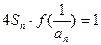 ,求数列通项an。(3)如果数列{bn}满足
,求数列通项an。(3)如果数列{bn}满足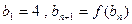 ,求证:当
,求证:当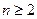 时,恒有
时,恒有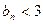 成立。
成立。(Ⅰ)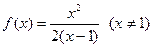 (Ⅱ)
(Ⅱ) 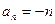 (Ⅲ)略
(Ⅲ)略
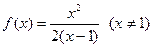 (Ⅱ)
(Ⅱ) 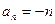 (Ⅲ)略
(Ⅲ)略:(1)设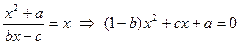 ∵0,2是方程
∵0,2是方程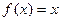 的根
的根
∴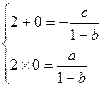 ∴
∴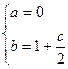 ∴
∴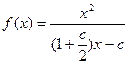
由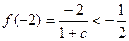 得
得 ∵
∵ ∴
∴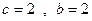 ∴
∴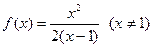
(2)由已知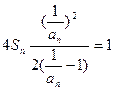 整理得
整理得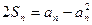
∴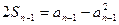 二式相减得
二式相减得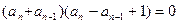
若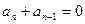 则当n=1时,
则当n=1时, (舍0)
(舍0)
则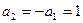 不合题意舍 若
不合题意舍 若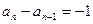 则{an}为首项-1,公差为-1的等差数列
则{an}为首项-1,公差为-1的等差数列
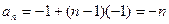 满足
满足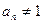 ∴
∴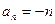
(3)由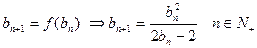
∴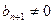 时,
时,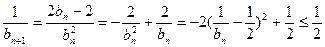
∴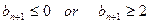 若
若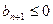 显然
显然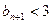 成立
成立
若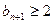 ,
,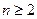 时则
时则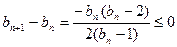
∴{bn}在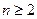 时单调递减∵
时单调递减∵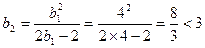 ∴
∴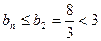
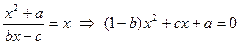 ∵0,2是方程
∵0,2是方程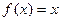 的根
的根 ∴
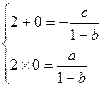 ∴
∴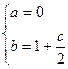 ∴
∴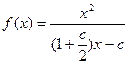
由
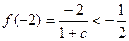 得
得 ∵
∵ ∴
∴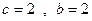 ∴
∴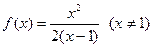
(2)由已知
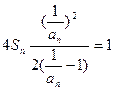 整理得
整理得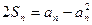
∴
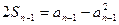 二式相减得
二式相减得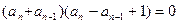
若
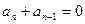 则当n=1时,
则当n=1时, (舍0)
(舍0)则
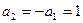 不合题意舍 若
不合题意舍 若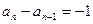 则{an}为首项-1,公差为-1的等差数列
则{an}为首项-1,公差为-1的等差数列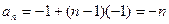 满足
满足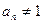 ∴
∴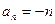
(3)由
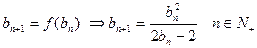
∴
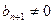 时,
时,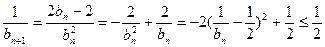
∴
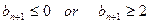 若
若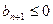 显然
显然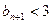 成立
成立若
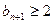 ,
,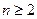 时则
时则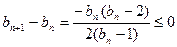
∴{bn}在
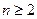 时单调递减∵
时单调递减∵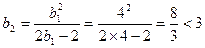 ∴
∴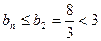

练习册系列答案
相关题目
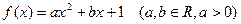 ,设方程
,设方程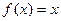 的两个实数根为
的两个实数根为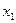 和
和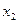 .
. 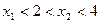 ,设函数
,设函数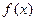 的对称轴为
的对称轴为 ,求证:
,求证: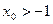 ;
;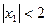 ,
,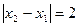 ,求
,求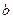 的取值范围.
的取值范围.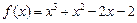 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下: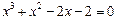 的一个近似根(精确到0.1)为( ).
的一个近似根(精确到0.1)为( ). 上以2为周期的函数,对
上以2为周期的函数,对 ,用
,用 表示区间
表示区间 已知当
已知当 时,f(x)=x2.
时,f(x)=x2. 不等的实根}
不等的实根}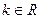 ,方程
,方程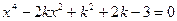 的实数x的取值范围是___ _______.
的实数x的取值范围是___ _______. 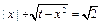 有相异实根的个数是( )
有相异实根的个数是( ) ,则方程
,则方程 在下面哪个区间内必有实根( )
在下面哪个区间内必有实根( )



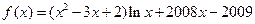 ,则方程
,则方程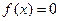 在下面哪个范围内必有实根( )
在下面哪个范围内必有实根( )