题目内容
已知直线l的参数方程: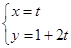 (t为参数)和圆C的极坐标方程:ρ=2
(t为参数)和圆C的极坐标方程:ρ=2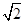 sin(θ+
sin(θ+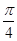 ).
).
(1)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;
(2)判断直线l和圆C的位置关系.
【答案】
(1)直线的普通方程为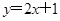 ,圆
,圆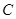 的直角坐标方程为
的直角坐标方程为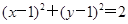 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)将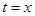 代入
代入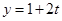 中,得直线的普通方程;极坐标方程和直角坐标方程互化关键是掌握
中,得直线的普通方程;极坐标方程和直角坐标方程互化关键是掌握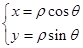 ,变形为
,变形为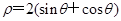 ,代入得
,代入得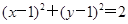 ;(2)利用直线和圆位置关系的几何判断,计算圆心
;(2)利用直线和圆位置关系的几何判断,计算圆心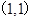 到直线的距离和圆的半径比较即可.
到直线的距离和圆的半径比较即可.
试题解析:(1)消去参数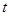 ,得直线
,得直线 的普通方程为
的普通方程为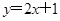 ,
,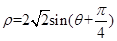 即
即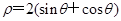 ,
,
两边同乘以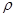 得
得
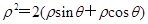 ,
,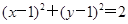 .
.
(2)圆心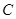 到直线
到直线 的距离
的距离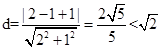 ,所以直线
,所以直线 和
和 相交.
相交.
考点:1、直线的参数方程和普通方程的互化;2、圆的极坐标方程和直角坐标方程的互化;3、直线和圆的位置关系.

练习册系列答案
相关题目