题目内容
1.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足asinB=$\sqrt{3}$bcosA.(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC周长的最大值.
分析 (Ⅰ)利用正弦定理、商的关系化简式子,求出tanA的值,由A的范围求出角A的大小;
(Ⅱ)解法一:由条件和余弦定理列出方程,利用基本不等式求出b+c的范围,再求出△ABC的周长最大值;
解法二:根据条件和正弦定理表示出b+c,利用两角和与差的正弦函数化简,求出B的范围,再由正弦函数的性质求出b+c的最大值,即可求出△ABC的周长最大值.
解答 解:(Ⅰ)依正弦定理可将$asinB=\sqrt{3}bcosA$化为:$sinAsinB=\sqrt{3}sinBcosA$…(2分)
因为在sinB>0中,sinB>0,
所以$sinA=\sqrt{3}cosA$,即$tanA=\sqrt{3}$,
∵0<A<π,∴$A=\frac{π}{3}$. …(5分)
(Ⅱ)因为=a+b+c=4+b+c的周长=a+b+c=4+b+c,
所以当b+c最大时,△ABC的周长最大,
解法一:因为a2=c2+b2-2bccosA=(b+c)2-3bc,…(7分)
因为a=4,且$bc≤\frac{{{{(b+c)}^2}}}{4}$,
∴16$≥\frac{{{{(b+c)}^2}}}{4}$,即b+c≤8(当且仅当b=c=4时等号成立) …(11分)
所以△ABC周长的最大值为12.…(12分)
解法二:因为$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{8\sqrt{3}}{3}$,
所以b+c=$\frac{8\sqrt{3}}{3}$(sinB+sinC)=$\frac{8\sqrt{3}}{3}$[sinB+sin($\frac{2π}{3}-B$)]
=$\frac{8\sqrt{3}}{3}$(sinB+sin$\frac{2π}{3}$cosB-cos$\frac{2π}{3}$sinB)
=$\frac{8\sqrt{3}}{3}$($\frac{3}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB)=8sin(B+$\frac{π}{6}$),
由$\frac{2π}{3}-B$<0得,0<B<$\frac{2π}{3}$,
当B=$\frac{π}{3}$时,8sin(B+$\frac{π}{6}$)=8,b+c取到最大值是8,
所以△ABC周长的最大值为12.
点评 本题考查正弦、余弦定理,两角和与差的正弦函数,正弦函数的性质,以及基本不等式求最值问题,属于中档题.

| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C. | $\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$ |
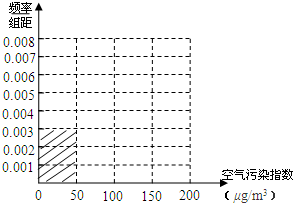 当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:
当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
| A. | 0 | B. | $\frac{1}{2}$ | C. | +∞ | D. | 2 |