题目内容
异面直线l与m上的单位方向向量分别为 ,
, ,且
,且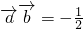 ,则l与m的夹角的大小为________°.
,则l与m的夹角的大小为________°.
60
分析:设两异面直线的夹角为 θ,则 cosθ=|cos<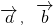 >|,由
>|,由 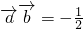 =1×1×cos<
=1×1×cos<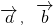 >,可得
>,可得
cos<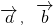 >的值,进而得到cosθ的值,从而得到θ 的值.
>的值,进而得到cosθ的值,从而得到θ 的值.
解答:由于异面直线的夹角的余弦值,等于分别位于两异面直线上的两个向量夹角的余弦值的绝对值,
设两异面直线的夹角为 θ,则 cosθ=|cos<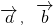 >|.
>|.
∵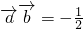 =1×1×cos<
=1×1×cos<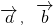 >,∴cos<
>,∴cos<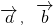 >=-
>=- ,∴cosθ=
,∴cosθ= ,θ=60°,
,θ=60°,
故答案为:60°.
点评:本题考查两个向量的数量积的定义,两异面直线所成的角的定义,判断两异面直线的夹角为 θ 与<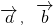 >的
>的
关系,时间诶体的关键.
分析:设两异面直线的夹角为 θ,则 cosθ=|cos<
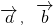 >|,由
>|,由 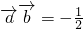 =1×1×cos<
=1×1×cos<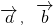 >,可得
>,可得 cos<
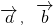 >的值,进而得到cosθ的值,从而得到θ 的值.
>的值,进而得到cosθ的值,从而得到θ 的值.解答:由于异面直线的夹角的余弦值,等于分别位于两异面直线上的两个向量夹角的余弦值的绝对值,
设两异面直线的夹角为 θ,则 cosθ=|cos<
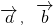 >|.
>|.∵
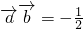 =1×1×cos<
=1×1×cos<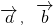 >,∴cos<
>,∴cos<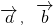 >=-
>=- ,∴cosθ=
,∴cosθ= ,θ=60°,
,θ=60°,故答案为:60°.
点评:本题考查两个向量的数量积的定义,两异面直线所成的角的定义,判断两异面直线的夹角为 θ 与<
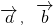 >的
>的关系,时间诶体的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x-2)
x-2)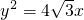 的焦点重合,对称轴为坐标轴,且经过点
的焦点重合,对称轴为坐标轴,且经过点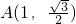 .
.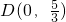 且斜率存在的直线l交椭圆E于M、N两点,线段MN的中点为Q,点B(-1,0),当l⊥QB时,求直线l的方程.
且斜率存在的直线l交椭圆E于M、N两点,线段MN的中点为Q,点B(-1,0),当l⊥QB时,求直线l的方程.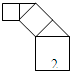 如图,正方形上连接等腰直角三角形,直角三角形边上再连接正方形,…,无限重复,设正方形的面积S1,S2,S3,…,三角形的面积为T1,T2,T3,…,当S1的边长为2时,这些正方形和三角形的面积总和为
如图,正方形上连接等腰直角三角形,直角三角形边上再连接正方形,…,无限重复,设正方形的面积S1,S2,S3,…,三角形的面积为T1,T2,T3,…,当S1的边长为2时,这些正方形和三角形的面积总和为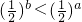
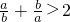 .
. ,an=2-
,an=2- (n≥2,n∈N*),数列 {bn},满足bn=
(n≥2,n∈N*),数列 {bn},满足bn= (n∈N*),
(n∈N*),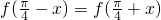 ,则直线ax+by+c=0的斜率为________.
,则直线ax+by+c=0的斜率为________.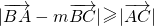 ,则△ABC为
,则△ABC为