��Ŀ����
������{xn}����xn��1�ң�n��N*����ǰn���ΪSn����֪��p1��x1��S1����P2��x2��s2������Pn��xn��sn������ֱ��y=kx+b�ϣ����г���b��k��k��1��b��0������yn=log
xn��
��1����֤������{xn]�ǵȱ����У�
��2����yn=18-3n����ʵ��k��b��ֵ��
��3���������t��s��N*��s��tʹ�õ㣨t��yt���͵㣨s��yt������ֱ��y=2x+1�ϣ����Ƿ����������M����n��Mʱ��xn��1������������ڣ����M����Сֵ���������ڣ���˵�����ɣ�
| 1 |
| 2 |
��1����֤������{xn]�ǵȱ����У�
��2����yn=18-3n����ʵ��k��b��ֵ��
��3���������t��s��N*��s��tʹ�õ㣨t��yt���͵㣨s��yt������ֱ��y=2x+1�ϣ����Ƿ����������M����n��Mʱ��xn��1������������ڣ����M����Сֵ���������ڣ���˵�����ɣ�
��1��֤�����ߵ�Pn��xn��Sn����Pn+1��xn+1��Sn+1������ֱ��y=kx+b�ϣ�
��Sn=kxn+b��Sn+1=kxn+1+b
��ʽ�����Sn+1-Sn=kxn+1-kxn����xn+1=kxn+1-kxn��
�߳���k��0����k��1����
=
�����㳣����
������{xn]�ǵȱ����У�
��2����yn=log0.5xn����xn=��
��yn=8n-6��
��
=8����k=
��
��Pn��ֱ���ϣ���Sn=kxn+b��
��n=1��b=S1-
x1=-
x1=-
��
��3����yn=log0.5xn���൱n��Mʱ��xn��1������ȼ���yn��0�������
�ߴ���t��s��N*��ʹ�ã�t��ys���ͣ�s��yt������y=2x+1�ϣ�
��ys=2t+1 �٣�yt=2s+1 �ڣ�
��-�ڵã�ys-yt=2��t-s����
��s��t����{yn}�ǹ���d=-2��0�ĵȲ�����
��+�ڵã�ys+yt=2��t+s��+2��
��ys+yt=y1+��s-1��•��-2��+y1+��t-1��•��-2��=2y1-2��s+t��+4
��2y1-2��s+t��+4=2��t+s��+2����y1=2��t+s��-1��0��
��������{yn}������Ϊ��������Ϊ���ĵȲ����У�
����һ������һ����С��Ȼ��M��ʹ
����
���t+s-
��M��t+s+
��
��M��N*����M=t+s��
��������Ȼ��M������СֵΪt+s��ʹ�õ�n��Mʱ��xn��1�������
��Sn=kxn+b��Sn+1=kxn+1+b
��ʽ�����Sn+1-Sn=kxn+1-kxn����xn+1=kxn+1-kxn��
�߳���k��0����k��1����
| xn+1 |
| xn |
| k |
| k-1 |
������{xn]�ǵȱ����У�
��2����yn=log0.5xn����xn=��
| 1 |
| 2 |
��
| k |
| k-1 |
| 8 |
| 7 |
��Pn��ֱ���ϣ���Sn=kxn+b��
��n=1��b=S1-
| 8 |
| 7 |
| 1 |
| 7 |
| 8-5 |
| 7 |
��3����yn=log0.5xn���൱n��Mʱ��xn��1������ȼ���yn��0�������
�ߴ���t��s��N*��ʹ�ã�t��ys���ͣ�s��yt������y=2x+1�ϣ�
��ys=2t+1 �٣�yt=2s+1 �ڣ�
��-�ڵã�ys-yt=2��t-s����
��s��t����{yn}�ǹ���d=-2��0�ĵȲ�����
��+�ڵã�ys+yt=2��t+s��+2��
��ys+yt=y1+��s-1��•��-2��+y1+��t-1��•��-2��=2y1-2��s+t��+4
��2y1-2��s+t��+4=2��t+s��+2����y1=2��t+s��-1��0��
��������{yn}������Ϊ��������Ϊ���ĵȲ����У�
����һ������һ����С��Ȼ��M��ʹ
|
|
���t+s-
| 1 |
| 2 |
| 1 |
| 2 |
��M��N*����M=t+s��
��������Ȼ��M������СֵΪt+s��ʹ�õ�n��Mʱ��xn��1�������

��ϰ��ϵ�д�
 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
�����Ŀ
�躯��f��x���������±�������{xn}����x=5���Ҷ�������Ȼ������xn+1=f��xn������x2012��ֵΪ�� ��
A��2
B��3
C��4
D��5
| x | 1 | 2 | 3 | 4 | 5 |
| f��x�� | 4 | 1 | 3 | 5 | 2 |
A��2
B��3
C��4
D��5
 ��
�� û��ʵ������
û��ʵ������ �ĵ������䣻
�ĵ������䣻 ����a=2��
����a=2�� ��֤����������m��N*����
��֤����������m��N*���� ��
��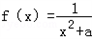 ��
��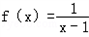 û��ʵ������
û��ʵ������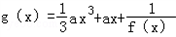 �ĵ������䣻
�ĵ������䣻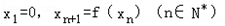 ����a=2��
����a=2�� ��֤����������m��N*����
��֤����������m��N*���� ��
��