题目内容
((本小题12分)已知函数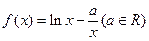 。
。
(1)判断 在定义域上的单调性;
在定义域上的单调性;
(2)若 在
在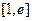 上的最小值为2,求
上的最小值为2,求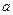 的值。
的值。
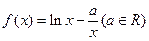 。
。(1)判断
 在定义域上的单调性;
在定义域上的单调性;(2)若
 在
在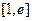 上的最小值为2,求
上的最小值为2,求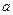 的值。
的值。解:(1)由题意得 的定义域为
的定义域为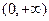 ,
,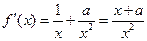 ……………………(2分)
……………………(2分)
①当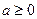 时,
时,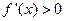 ,故
,故 在
在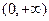 上为增函数…………………………(4分)
上为增函数…………………………(4分)
②当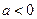 时,由
时,由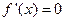 得
得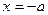 ;由
;由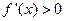 得
得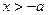 ;
;
由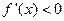 得
得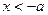 ;
;
∴ 在
在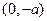 上为减函数;在
上为减函数;在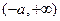 上为增函
上为增函 数.…………………………(6分)
数.…………………………(6分)
所以,当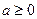 时,
时, 在
在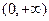 上是增函数;当
上是增函数;当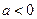 时,
时, 在
在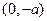 上是减函数,在
上是减函数,在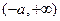 上是增函数…………………………………………………………………………(7分)
上是增函数…………………………………………………………………………(7分)
(2)∵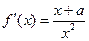 ,
,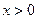 .由(1)可知:
.由(1)可知:
①当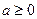 时,
时, 在
在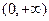 上为增函数,
上为增函数,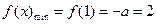 ,得
,得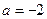 ,矛盾!
,矛盾!
…………………………………………………………………………………………(8分)
②当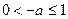 时,即
时,即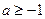 时,
时, 在
在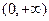 上也是增函数,
上也是增函数,
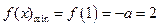 ,∴
,∴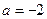 (舍去).………………………………………(9分)
(舍去).………………………………………(9分)
③当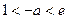 时,即
时,即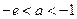 时,
时, 在
在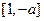 上是
上是 减函数,在
减函数,在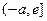 上是增函数,
上是增函数,
∴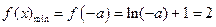 ,得
,得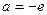 (舍去).………………………(10分)
(舍去).………………………(10分)
④当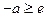 时,即
时,即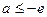 时,
时, 在
在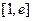 上是减函数,有
上是减函数,有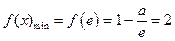 ,
,
∴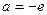 …………………………………………………………………………(11分)
…………………………………………………………………………(11分)
综上可知: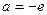 .……………………………………………………………………(12分)
.……………………………………………………………………(12分)
 的定义域为
的定义域为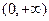 ,
,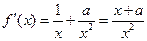 ……………………(2分)
……………………(2分)①当
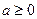 时,
时,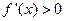 ,故
,故 在
在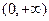 上为增函数…………………………(4分)
上为增函数…………………………(4分)②当
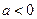 时,由
时,由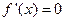 得
得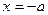 ;由
;由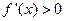 得
得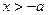 ;
;由
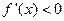 得
得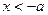 ;
;∴
 在
在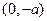 上为减函数;在
上为减函数;在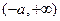 上为增函
上为增函 数.…………………………(6分)
数.…………………………(6分)所以,当
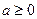 时,
时, 在
在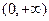 上是增函数;当
上是增函数;当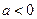 时,
时, 在
在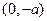 上是减函数,在
上是减函数,在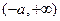 上是增函数…………………………………………………………………………(7分)
上是增函数…………………………………………………………………………(7分)(2)∵
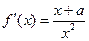 ,
,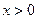 .由(1)可知:
.由(1)可知:①当
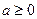 时,
时, 在
在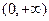 上为增函数,
上为增函数,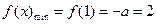 ,得
,得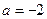 ,矛盾!
,矛盾!…………………………………………………………………………………………(8分)
②当
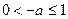 时,即
时,即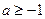 时,
时, 在
在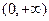 上也是增函数,
上也是增函数,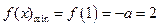 ,∴
,∴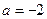 (舍去).………………………………………(9分)
(舍去).………………………………………(9分)③当
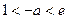 时,即
时,即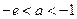 时,
时, 在
在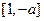 上是
上是 减函数,在
减函数,在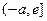 上是增函数,
上是增函数,∴
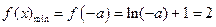 ,得
,得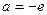 (舍去).………………………(10分)
(舍去).………………………(10分)④当
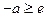 时,即
时,即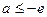 时,
时, 在
在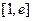 上是减函数,有
上是减函数,有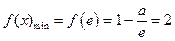 ,
,∴
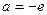 …………………………………………………………………………(11分)
…………………………………………………………………………(11分)综上可知:
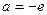 .……………………………………………………………………(12分)
.……………………………………………………………………(12分)略

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
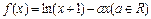
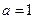 时,求
时,求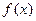 在定义域上的最大值;
在定义域上的最大值;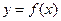 在
在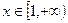 上恒有
上恒有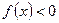 ,求
,求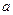 的取值范围;
的取值范围;
 在点
在点 处的切线方程为( )
处的切线方程为( ) B
B C
C D
D 
 在点
在点 处的切线方程为( )
处的切线方程为( )



 +
+ +
+ =
= ,
, +
+ +
+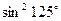 =
=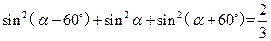
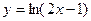 上的点到直线
上的点到直线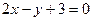 的最短距离是( )
的最短距离是( )


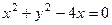 在点
在点 处的切线方程为( )
处的切线方程为( )

 B
B
 D
D
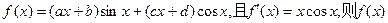 = 。
= 。