题目内容
若定义在R上的函数对任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2)-1成立,且当x>0时,f(x)>1,若f(4)=5,则不等式f(3m-2)<3的解集为
(-∞,
)
| 4 |
| 3 |
(-∞,
)
.| 4 |
| 3 |
分析:根据题意证出f(0)=1,进而证出F(x)=f(x)-1为奇函数.利用函数单调性的定义,结合题中的条件证出 F(x)=f(x)-1是R上的增函数,因此y=f(x)也是R上的增函数.由f(4)=5代入题中等式算出f(2)=3,将原不等式转化为f(3m-2)<f(2),利用单调性即可求出原不等式的解集.
解答:解:由题意,可得
令x1=x2=0,则f(0+0)=f(0)+f(0)-1,可得f(0)=1,
令x1=-x,x2=x,则f[(-x)+x]=f(-x)+f(x)-1=1,
∴化简得:[f(x)-1]+[f(-x)-1]=0,
∴记F(x)=f(x)-1,可得F(-x)=-F(x),即F(x)为奇函数.
任取x1,x2∈R,且x1>x2,则x1-x2>0,
F(x1)-F(x2)=F(x1)+F(-x2)=[f(x1)-1]+[f(-x2)-1]
=[f(x1)+f(-x2)-2]=[f(x1-x2)-1]=F(x1-x2)
∵当x>0时f(x)>1,可得x>0时,F(x)=f(x)-1>0,
∴由x1-x2>0,得F(x1-x2)>0,即F(x1)>F(x2).
∴F(x)=f(x)-1是R上的增函数,因此函数y=f(x)也是R上的增函数.
∵f(x1+x2)=f(x1)+f(x2)-1,且f(4)=5,
∴f(4)=f(2)+f(2)-1=5,可得f(2)=3.
因此,不等式f(3m-2)<3化为f(3m-2)<f(2),
可得3m-2<2,解之得m<
,即原不等式的解集为(-∞,
).
令x1=x2=0,则f(0+0)=f(0)+f(0)-1,可得f(0)=1,
令x1=-x,x2=x,则f[(-x)+x]=f(-x)+f(x)-1=1,
∴化简得:[f(x)-1]+[f(-x)-1]=0,
∴记F(x)=f(x)-1,可得F(-x)=-F(x),即F(x)为奇函数.
任取x1,x2∈R,且x1>x2,则x1-x2>0,
F(x1)-F(x2)=F(x1)+F(-x2)=[f(x1)-1]+[f(-x2)-1]
=[f(x1)+f(-x2)-2]=[f(x1-x2)-1]=F(x1-x2)
∵当x>0时f(x)>1,可得x>0时,F(x)=f(x)-1>0,
∴由x1-x2>0,得F(x1-x2)>0,即F(x1)>F(x2).
∴F(x)=f(x)-1是R上的增函数,因此函数y=f(x)也是R上的增函数.
∵f(x1+x2)=f(x1)+f(x2)-1,且f(4)=5,
∴f(4)=f(2)+f(2)-1=5,可得f(2)=3.
因此,不等式f(3m-2)<3化为f(3m-2)<f(2),
可得3m-2<2,解之得m<
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题给出抽象函数满足的条件,求解关于m的不等式.着重考查了函数的简单性质及其应用、不等式的解法等知识,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
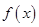 对任意的
对任意的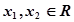 ,都有
,都有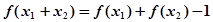 成立,且当
成立,且当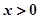 时,
时,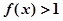 .
.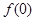 的值;(2)求证:
的值;(2)求证: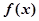 是R上的增函数;
是R上的增函数;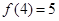 ,不等式
,不等式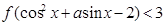 对任意的
对任意的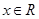 恒成立,求实数
恒成立,求实数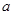 的取值范围.
的取值范围.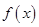 对任意的
对任意的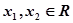 ,都有
,都有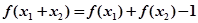 成立,且当
成立,且当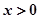 时,
时, 。
。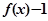 为奇函数;
为奇函数;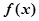 是R上的增函数;
是R上的增函数;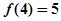 ,解不等式
,解不等式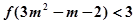 .
.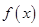 对任意的
对任意的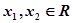 ,都有
,都有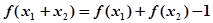 成立,且当
成立,且当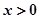 时,
时,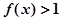 。
。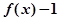 为奇函数;
为奇函数;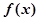 是R上的增函数;
是R上的增函数;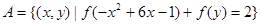 ,
,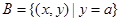 ,且
,且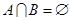 ,
求实数
,
求实数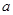 的取值范围。
的取值范围。