题目内容
若对一切实数x,二次函数f(x)=ax2+bx+c(a≠0)的值恒为非负实数,则| b+c | a |
分析:先有条件找到a,b,c须满足的条件,把
转化为
+
,再利用二次函数的最值可以求
的最小值
| b+c |
| a |
| b2 |
| 4a2 |
| b |
| a |
| b+c |
| a |
解答:解:二次函数f(x)=ax2+bx+c(a≠0)的值恒为非负实数,
即为所有函数值大于等于0,故须
?
?b2≤4ac?c≥
?b+c≥
+ b?
≥
+
,
设G=
+
=
(
+2)2-1≥-1,即
的最小值为-1
故答案为-1.
即为所有函数值大于等于0,故须
|
|
| b2 |
| 4a |
?b+c≥
| b2 |
| 4a |
| b+c |
| a |
| b2 |
| 4a2 |
| b |
| a |
设G=
| b2 |
| 4a2 |
| b |
| a |
| 1 |
| 4 |
| b |
| a |
| b+c |
| a |
故答案为-1.
点评:二次函数中的恒成立问题,一般分为两类:一是大于0恒成立,须开口向上且判别式小于0;二是小于0恒成立,须开口向下且判别式小于0

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
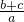 的最小值是 ________.
的最小值是 ________.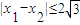 .
.