题目内容
某公司为了适应市场需求对产品结构做了重大调整，调整后初期利润增长迅速，之后增长越来越慢，若要建立恰当的函数模型来反映该公司调整后利润
与时间
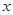的关系，可选用（ ）
| A．一次函数 | B．二次函数 | C．指数型函数 | D．对数型函数 |
D
解析试题分析：根据基本初等函数的图像与性质可知，一次函数增长的速度一直保持同样，不满足题意；要满足调整后初期利润增长迅速，如果是二次函数，则必须开口向上，而此时在二次函数对称轴的右侧增长的速度是越来越快，没有慢下来的可能，不符合要求；要满足调整后初期利润增长迅速，如果是指数函数，则底数必是大于1的数，而此时指数函数增长的迅速也是越来越快的，也不满足要求；对于对数函数，当底数大于1时，对数函数增长的速度先快后慢，符合要求，故选D.
考点：1.函数模型及其应用；2.基本初等函数的图像与性质.
练习册系列答案
53随堂测系列答案
相关题目
种计算机病毒是通过电子邮件进行传播的，下表是某公司前5天监测到的数据：
第 天 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 （台） | 10 | 20 | 39 | 81 | 160 |
天被感染的数量与之间的关系的是（ ）A．
B．
C．
D．
已知函数
，若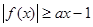
恒成立，则实数a的取值范围是（ ）
A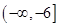． | B． |
C． | D． |
，专家预测经过
年可能增长到原来的
倍，则函数的图像大致为（ ）
函数
的零点所在区间是（ ）
A． | B． | C． | D． |
若
，则
的表达式为（ ）
A． | B． | C． | D． |
函数
的图象为曲线
，函数
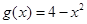的图象为曲线
，过
轴上的动点
作垂直于轴的直线分别交曲线，于
两点，则线段
长度的最大值为（ ）
| A．2 | B．4 | C．5 | D． |
某校要召开学生代表大会，规定各班每10人推选一名代表，当班人数除以10的余数大于6时，再增选一名代表，则各班推选代表人数
与该班人数
之间的函数关系用取整函数
（
表示不大于的最大整数，如
）可表示为（ ）
A． | B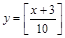． | C． | D． |
设函数f(x)的零点为x1，函数g(x)＝4x＋2x－2的零点为x2，若|x1－x2|>
，则f(x)可以是( )．
A．f(x)＝2x－ | B．f(x)＝－x2＋x－ |
| C．f(x)＝1－10x | D．f(x)＝ln (8x－2) |