题目内容
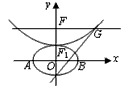
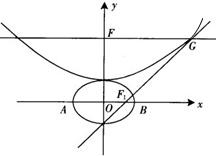
设b>0,椭圆方程为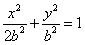 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
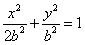 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
解:(1)由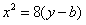 得
得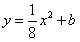 ,
,
当y=b+2得x=±4,∴G点的坐标为(4,b+2),
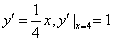 ,
,
过点G的切线方程为y-(b+2)=x-4即y=x+b-2,
令y=0得x=2-b,
∴F1点的坐标为(2-b,0),
由椭圆方程得F1点的坐标为(b,0),
∴2-b=b即b=1,
即椭圆和抛物线的方程分别为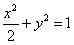 和
和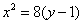 ;
;
(2)∵过A作x轴的垂线与抛物线只有一个交点P,
∴以∠PAB为直角的Rt△ABP只有一个,
同理以∠PAB为直角的Rt△ABP只有一个。
若以∠PAB为直角,设P点坐标为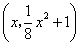 ,A、B两点的坐标分别为
,A、B两点的坐标分别为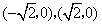 ,
,
由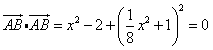 得
得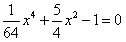 ,
,
关于x2的一元二次方程有一解,
∴x有二解,即以∠APB为直角的Rt△ABP有二个;
因此抛物线上共存在4个点使△ABP为直角三角形.
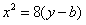 得
得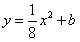 ,
,当y=b+2得x=±4,∴G点的坐标为(4,b+2),
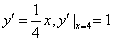 ,
,过点G的切线方程为y-(b+2)=x-4即y=x+b-2,
令y=0得x=2-b,
∴F1点的坐标为(2-b,0),
由椭圆方程得F1点的坐标为(b,0),
∴2-b=b即b=1,
即椭圆和抛物线的方程分别为
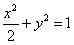 和
和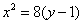 ;
; (2)∵过A作x轴的垂线与抛物线只有一个交点P,
∴以∠PAB为直角的Rt△ABP只有一个,
同理以∠PAB为直角的Rt△ABP只有一个。
若以∠PAB为直角,设P点坐标为
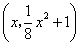 ,A、B两点的坐标分别为
,A、B两点的坐标分别为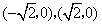 ,
,由
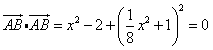 得
得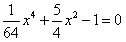 ,
,关于x2的一元二次方程有一解,
∴x有二解,即以∠APB为直角的Rt△ABP有二个;
因此抛物线上共存在4个点使△ABP为直角三角形.

练习册系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为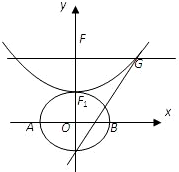 设b>0,椭圆方程为
设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.