题目内容
三棱锥三条侧棱两两垂直,长度分别是1、
、2,则其外接球的表面积是( )
| 3 |
| A、8π | ||||
| B、16π | ||||
C、
| ||||
| D、32π |
考点:球的体积和表面积,球内接多面体
专题:计算题,空间位置关系与距离
分析:由已知中三棱锥的三条侧棱两两相互垂直,故可将其补充为一个长方体,根据外接球的直径等于长方体的对角线,求出球的半径,代入球的表面积公式,即可求出答案.
解答:
解:∵三棱锥的三条侧棱两两相互垂直,且三条侧棱长分别是1、
、2,
∴可将其补充为一个长宽高分别是1、
、2的长方体,
∴其外接球的直径2R=2
,
三棱锥的外接球的表面积S=4πR2=8π
故选:A.
| 3 |
∴可将其补充为一个长宽高分别是1、
| 3 |
∴其外接球的直径2R=2
| 2 |
三棱锥的外接球的表面积S=4πR2=8π
故选:A.
点评:本题考查球的表面积,构造长方体,求出其外接球的半径是解答本题的关键.

练习册系列答案
相关题目
下列函数中,增长速度最快的是( )
| A、y=20x |
| B、y=x20 |
| C、y=log20x |
| D、y=20x |
 如图,在正方体ABCD-A1B1C1D1中,线段AD1、B1C所在直线的位置关系是( )
如图,在正方体ABCD-A1B1C1D1中,线段AD1、B1C所在直线的位置关系是( )| A、平行 | B、相交且垂直 |
| C、异面但不垂直 | D、异面且垂直 |
函数f(x)=(
)x-cosx在区间[0,2π]上的零点个数是( )
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
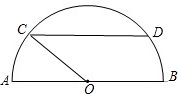 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧