题目内容
已知: 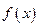 是定义在区间
是定义在区间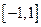 上的奇函数,且
上的奇函数,且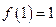 .若对于任意的
.若对于任意的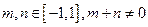 时,都有
时,都有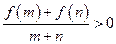 .
.
(1)解不等式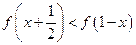 .
.
(2)若 对所有
对所有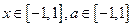 恒成立,求实数
恒成立,求实数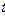 的取值范围
的取值范围
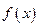 是定义在区间
是定义在区间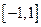 上的奇函数,且
上的奇函数,且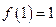 .若对于任意的
.若对于任意的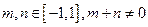 时,都有
时,都有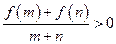 .
.(1)解不等式
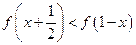 .
.(2)若
 对所有
对所有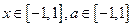 恒成立,求实数
恒成立,求实数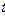 的取值范围
的取值范围(1)令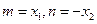 则有
则有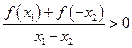 ,即
,即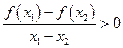 .
.
当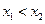 时,必有
时,必有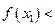
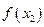
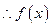 在区间
在区间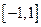 上是增函数
上是增函数
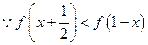
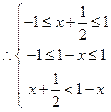 解之
解之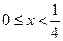
所求解集为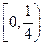
(2)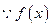 在区间
在区间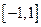 上是增函数,
上是增函数, 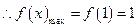
又对于所有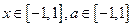 ,
, 恒成立
恒成立
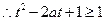 ,即
,即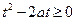 在
在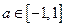 时恒成立
时恒成立
记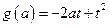 ,则有
,则有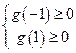 即
即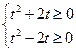
解之得,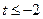 或
或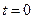 或
或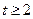
 的取值范围是
的取值范围是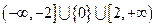
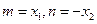 则有
则有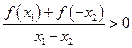 ,即
,即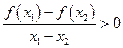 .
.当
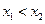 时,必有
时,必有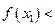
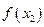
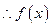 在区间
在区间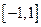 上是增函数
上是增函数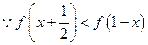
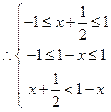 解之
解之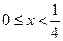
所求解集为
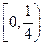
(2)
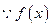 在区间
在区间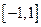 上是增函数,
上是增函数, 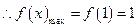
又对于所有
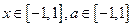 ,
, 恒成立
恒成立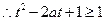 ,即
,即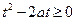 在
在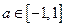 时恒成立
时恒成立记
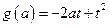 ,则有
,则有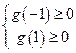 即
即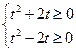
解之得,
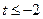 或
或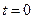 或
或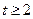
 的取值范围是
的取值范围是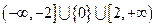
略

练习册系列答案
相关题目
 是偶函数,则有序实数对(
是偶函数,则有序实数对(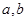 )可以是 . (写出你认为正确的一组数即可)
)可以是 . (写出你认为正确的一组数即可)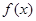 是定义域为
是定义域为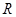 的奇函数,当
的奇函数,当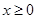 时,
时,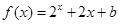 (
(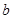 为常数),则
为常数),则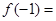 ( )
( )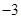
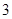
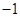
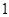
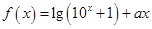 是偶函数,那么
是偶函数,那么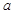 的值为 ( )
的值为 ( )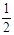
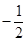
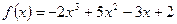 ,则
,则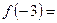
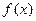 是定义
是定义 在R上的奇函数, 而且单调递增,若实数
在R上的奇函数, 而且单调递增,若实数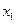 ,
, 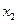 ,
, 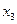 满足
满足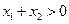 ,
, 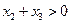 ,
, 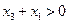 , 给出下面四个结论:
, 给出下面四个结论: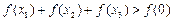 ;②
;②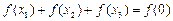 ;
;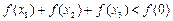 ; ④
; ④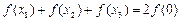
 (只填序号)
(只填序号)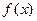 是满足
是满足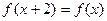 的奇函数,当
的奇函数,当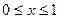 时,
时,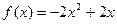 ,则
,则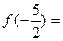
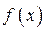 满足
满足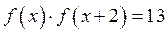 ,若
,若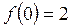 ,则
,则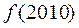 =__
=__