题目内容
13.数列{an}为等差数列,a1=30,d=-0.6.(1)从第几项开始有an<0;
(2)求此数列的前n项和的最大值.
分析 (1)求出数列的通项公式,解不等式an<0即可;
(2)根据等差数列前n项和的性质即可求此数列的前n项和的最大值.
解答 解:(1)∵a1=30,d=-0.6,
∴an=30-0.6(n-1)=-0.6n+30.6.
令-0.6n+30.6<0,则n>$\frac{30.6}{0.6}$=51.
由于n∈N*,故当n≥52时,an<0即从第52项开始,以后各项an<0;
(2)∵d=-0.6<0,a1=30>0,
∴由an=-0.6n+30.6≥0,
得n≤51,即前51项和最大,.
∴(Sn)max=S51=51×30+$\frac{51×50}{2}×$(-0.6)=1530-765=765.
点评 本题主要考查等差数列的通项公式以及前n项和公式的求解,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若直线l:ax+by=0与圆C:x2+y2-4x+4y=0相交,则直线l的倾斜角不等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{6}$ |
5.某研究小组为了研究中学生的身体发育情况,在某学校随机抽出20名15至16周岁的男生,将他们的身高和体重制成2×2的列联表,根据列联表的数据,判断该学校15至16周岁的男生的身高和体重之间在犯错误概率不超过0.025的前提下有关系.
附:独立性检验临界值表
k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 超重 | 不超重 | 总计 | |
| 偏高 | 1 | 1 | 5 |
| 不偏高 | 3 | 12 | 15 |
| 总计 | 7 | 12 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
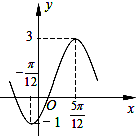 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的部分图象如图所示.