题目内容
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据椭圆的几何性质得到a=![]() c,bc=1,解得方程;(2)设椭圆上一点为.P(
c,bc=1,解得方程;(2)设椭圆上一点为.P(![]() cos θ,sin θ),用点点距离表示|PF|+|PM|,最终求得定值。
cos θ,sin θ),用点点距离表示|PF|+|PM|,最终求得定值。
解析:
(1)解 由题意可知:椭圆的离心率e=![]() ,则a=
,则a=![]() c.
c.
由△AOF的面积为S=![]() ×b×c=
×b×c=![]() ,则bc=1,
,则bc=1,
由a2=b2+c2,解得a=![]() ,b=c=1.
,b=c=1.
∴椭圆的标准方程为![]() ;.
;.
(2)证明 由(1)知:F(1,0),以椭圆的短轴为直径的圆的方程为x2+y2=1,
设P(![]() cos θ,sin θ),且cos θ>0,
cos θ,sin θ),且cos θ>0,
则|PF|=![]() =
=
由M是圆x2+y2=1的切点,则OM⊥PM,且|OM|=1,
则|PM|=![]() =cos θ,
=cos θ,
∴|PF|+|PM|=![]() -cos θ+cos θ=
-cos θ+cos θ=![]() ,
,
∴|PF|+|PM|为定值.

【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 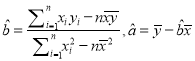 .
.
参考数据: ![]() .
.