题目内容
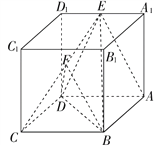
【题目】如图，正方体ABCD－A1B1C1D1中，点E是A1D1的中点，点F是CE的中点．
(Ⅰ)求证：平面ACE⊥平面BDD1B1；
(Ⅱ)求证：AE∥平面BDF.
【答案】(1)见解析(2)见解析
【解析】试题分析：（Ⅰ）通过证明AC⊥平面BDD1B1，即可证明平面ACE⊥平面BDD1B1；
（Ⅱ）通过证明OF∥AE，即可证明AE∥平面BDF．
试题解析：
(Ⅰ)在正方体中，ABCD是正方形，BB1⊥平面ABCD，
∴AC⊥BD，AC⊥BB1，
∵BD∩BB1＝B，BD，
BB1平面BDD1B1，
∴AC⊥平面BDD1B1，
∵AC平面ACE，∴平面ACE⊥平面BDD1B1.6分
(Ⅱ)连AC交BD于G，连FG，
∵ABCD是正方形，∴G是AC中点，
∵F是CE是中点，∴AE∥FG，
∵AE平面BDF，FG平面BDF，
∴AE∥平面BDF.
练习册系列答案
相关题目
【题目】某种产品按质量标准分为
,
,
,
,
五个等级.现从一批该产品随机抽取20个，对其等级进行统计分析，得到频率分布表如下：
等级 |
|
|
|
|
|
频率 |
|
|
|
|
|
（1）在抽取的20个产品中，等级为5的恰有2个，求
,
；
（2）在（1）的条件下，从等级为3和5的所有产品中，任意抽取2个，求抽取的2个产品等级恰好相同的概率.
