题目内容
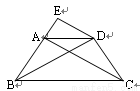
如图，等腰梯形ABCD中，E，F分别是BC上三等分点，AD=AE=1，BC=3，若把三角形ABE和DCF分别沿AE和DF折起，使得B、C两点重合于一点P，则二面角P-AD-E的大小为 ．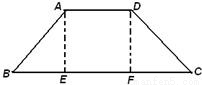
【答案】分析：在折叠问题中注意到一些长度和角度的不变性，易看出面PEF⊥底面AEFD，故二面角P-AD-E的平面角可由三垂线定理法作出，然后在直角三角形中求解即可．
解答：解：由原图可知BE⊥AE，CF⊥DF，所以在折叠的图形中有PE⊥AE，PF⊥DF，
因为AE∥DF，所以AE⊥面PEF，所以面PEF⊥底面AEFD．
分别取EF和AD的中点M、N，则PN⊥EF，从而PN⊥底面AEFD，因为MN⊥EF，
所以∠PMN即为二面角P-AD-E的平面角，
因为MN=AE=1，PN=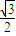
，所以tan∠PMN=
，
所以二面角P-AD-E的大小为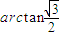
，
故答案为：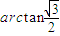
．
点评：本题考查折叠问题、二面角的做法和求解，考查空间想象能力和运算能力．
解答：解：由原图可知BE⊥AE，CF⊥DF，所以在折叠的图形中有PE⊥AE，PF⊥DF，
因为AE∥DF，所以AE⊥面PEF，所以面PEF⊥底面AEFD．
分别取EF和AD的中点M、N，则PN⊥EF，从而PN⊥底面AEFD，因为MN⊥EF，
所以∠PMN即为二面角P-AD-E的平面角，
因为MN=AE=1，PN=
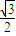，所以tan∠PMN=，所以二面角P-AD-E的大小为
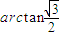，故答案为：
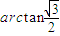．点评：本题考查折叠问题、二面角的做法和求解，考查空间想象能力和运算能力．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（2013•惠州一模）如图，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，∠BAC=∠ACD=90°，AE∥CD，DC=AC=2AE=2
