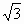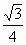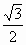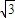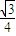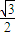题目内容
有一个四棱锥,底面是一个等腰梯形,并且腰长和较短的底长都是1,有一个底角是60°,又侧棱与底面所成的角都是45°,则这个棱锥的体积是
- A.1
- B.

- C.

- D.

C
分析:如图,容易求出底面等腰梯形ABCD的面积.利用侧棱与底面所成的角都是45°,确定出顶点P在底面的射为RT△BAC外心.即为BC中点O,得出高PO,利用锥体体积公式计算即可.
解答: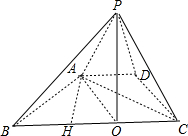 解:如图,在等腰梯形ABCD中,AD=AB=DC=1,∠ABC=60°,过A作AH⊥BC于H,
解:如图,在等腰梯形ABCD中,AD=AB=DC=1,∠ABC=60°,过A作AH⊥BC于H,
则BH=BA•cos60°= .AH=
.AH= .
.
根据等腰梯形的性质,下底BC=AD+2BH=2.设O为BC中点,则BO=OC=1,△ABO为正三角形,∠BAO=60°,△AOC为等腰三角形,∠OAC=30°,
∴∠BAC=90°.
因为侧棱与底面所成的角都是45°,所以顶点P在底面的射影到ABCD各顶点的距离相等,即为等腰梯形ABCD 的外接圆的圆心,也为RT△BAC外心,即为点O,
∴PO为四棱锥的高.PO=OC=1.
又S梯形ABCD= (AD+BC)×AH=
(AD+BC)×AH=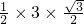 =
=
∴锥体体积V= S梯形ABCD×PO=
S梯形ABCD×PO=
故选C.
点评:本题考查锥体体积的计算,考查空间想象能力、转化、计算、推理论证能力.关键是确定出顶点P在底面的射为RT△BAC外心.
分析:如图,容易求出底面等腰梯形ABCD的面积.利用侧棱与底面所成的角都是45°,确定出顶点P在底面的射为RT△BAC外心.即为BC中点O,得出高PO,利用锥体体积公式计算即可.
解答:
 解:如图,在等腰梯形ABCD中,AD=AB=DC=1,∠ABC=60°,过A作AH⊥BC于H,
解:如图,在等腰梯形ABCD中,AD=AB=DC=1,∠ABC=60°,过A作AH⊥BC于H,则BH=BA•cos60°=
 .AH=
.AH= .
.根据等腰梯形的性质,下底BC=AD+2BH=2.设O为BC中点,则BO=OC=1,△ABO为正三角形,∠BAO=60°,△AOC为等腰三角形,∠OAC=30°,
∴∠BAC=90°.
因为侧棱与底面所成的角都是45°,所以顶点P在底面的射影到ABCD各顶点的距离相等,即为等腰梯形ABCD 的外接圆的圆心,也为RT△BAC外心,即为点O,
∴PO为四棱锥的高.PO=OC=1.
又S梯形ABCD=
 (AD+BC)×AH=
(AD+BC)×AH=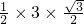 =
=
∴锥体体积V=
 S梯形ABCD×PO=
S梯形ABCD×PO=
故选C.
点评:本题考查锥体体积的计算,考查空间想象能力、转化、计算、推理论证能力.关键是确定出顶点P在底面的射为RT△BAC外心.

练习册系列答案
相关题目