题目内容
设 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则数列
,则数列 的通项公式为( )
的通项公式为( )
A.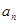 =2n-3 =2n-3 | B.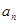 =2n-1 =2n-1 | C.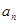 =2n+1 =2n+1 | D.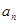 =2n+3 =2n+3 |
C
解析试题分析:根据题意,由于等差数列 的
的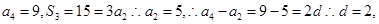 则数列
则数列 的通项公式为
的通项公式为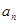 =
=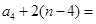 2n+1,故选C.
2n+1,故选C.
考点:等差数列通项公式
点评:本题主要考查等差数列通项公式和构造数列裂项法求和,是数列中常考的问题

练习册系列答案
相关题目
已知等差数列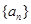 中,
中, ,
,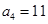 ,则前10项和
,则前10项和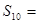 ( )
( )
| A.55 | B.155 | C.350 | D.400 |
已知等比数列{an}中a2=1,则其前3项的和S3的取值范围是( )
| A.(-∞,-1] | B.(-∞,0)∪(1,+∞) |
| C.[3,+∞) | D.(-∞,-1]∪[3,+∞) |
设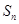 为等差数列
为等差数列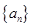 的前
的前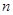 项和,若
项和,若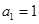 ,公差
,公差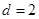 ,
, 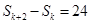 ,则
,则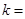 ( )
( )
| A.8 | B.7 | C.6 | D.5 |
在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于( )
| A.45 | B.75 |
| C.300 | D.180 |
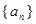 为等差数列,
为等差数列,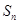 为其前
为其前 项和,
项和,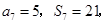 则
则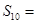
A.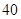 | B.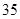 | C.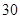 | D.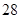 |
如果等差数列 中,
中, ,那么
,那么 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
数列1,3,6,10,…的一个通项公式an= ( )
| A.n2-n+1 | B. | C. | D. |
已知等差数列 中,
中,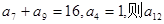 的值是( )
的值是( )
A.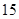 | B. | C.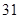 | D. |