题目内容
如果等差数列 中,
中, ,那么
,那么 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
C
解析试题分析:因为 ,所以
,所以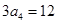 ,所以
,所以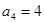 ,
,
故 =
=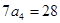 .选C.
.选C.
考点:等差数列的通项公式 等式数列的性质
点评:本题主要考察等差数列的性质,利用性质进行转化是解题的关键, 属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示程序框图所表达的算法,输出的结果是( )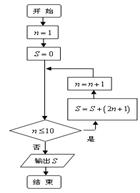
| A.99 | B.100 | C.120 | D.142 |
设 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列,则
成等比数列,则 等于
等于
| A.1 | B.2 | C.3 | D.4 |
设 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则数列
,则数列 的通项公式为( )
的通项公式为( )
A.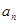 =2n-3 =2n-3 | B.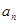 =2n-1 =2n-1 | C.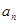 =2n+1 =2n+1 | D.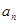 =2n+3 =2n+3 |
设等差数列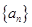 满足
满足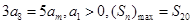 ,则m的值为 ( )
,则m的值为 ( )
A. | B.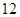 | C. | D.26 |
设等差数列 的前
的前 项和为
项和为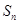 且满足
且满足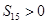 ,
,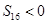 ,则
,则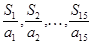 中最大的项为
中最大的项为
A. | B. | C.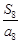 | D. |
已知两个等差数到 和
和 的前
的前 项和分别为
项和分别为 和
和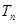 ,且
,且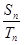 =
= ,则
,则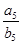 =( )
=( )
| A.3 | B.4 | C.5 | D.6 |
两数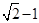 与
与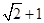 等差中项是( )
等差中项是( )
A. | B.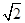 | C.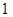 | D.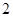 |
类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
| A.连续两项的和相等的数列叫等和数列 |
| B.从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列 |
| C.从第二项起,以后每一项与前一项的和都相等的数列叫等和数列 |
| D.从第一项起,以后每一项与前一项的和都相等的数列叫等和数列 |