题目内容
在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于( )
| A.45 | B.75 |
| C.300 | D.180 |
D
解析试题分析:据等差数列的性质可知,项数之和相等的两项之和相等,化简已知的等式即可求出a5的值,然后把所求的式子也利用等差数列的性质化简后,将a5的值代入即可求出值解:由a3+a4+a5+a6+a7=(a3+a7)+(a4+a6)+a5=5a5=450,得到a5=90,则a2+a8=2a5=180.故答案为:D
考点:等差数列的性质
点评:此题考查学生灵活运用等差数列的性质化简求值,是一道基础题.学生化简已知条件时注意项数之和等于10的两项结合.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知数列{ }是公差为3的等差数列,且
}是公差为3的等差数列,且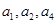 成等比数列,则
成等比数列,则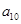 等于( )
等于( )
| A.30 | B.27 | C.24 | D.33 |
已知等差数列 中
中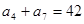 ,则前10项和
,则前10项和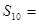 ( )
( )
| A.420 | B.380 | C.210 | D.140 |
设 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列,则
成等比数列,则 等于
等于
| A.1 | B.2 | C.3 | D.4 |
在等差数列3,8,13…中,第5项为( ).
| A.15 | B.18 | C.19 | D.23 |
设 是等差数列
是等差数列 的前n项和,若
的前n项和,若 ,则数列
,则数列 的通项公式为( )
的通项公式为( )
A.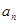 =2n-3 =2n-3 | B.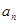 =2n-1 =2n-1 | C.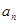 =2n+1 =2n+1 | D.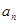 =2n+3 =2n+3 |
设等差数列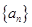 满足
满足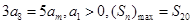 ,则m的值为 ( )
,则m的值为 ( )
A. | B.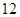 | C. | D.26 |
已知两个等差数到 和
和 的前
的前 项和分别为
项和分别为 和
和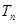 ,且
,且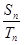 =
= ,则
,则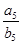 =( )
=( )
| A.3 | B.4 | C.5 | D.6 |
已知数列 是等差数列,若
是等差数列,若 ,则数列
,则数列 的公差等于
的公差等于
| A.1 | B.3 | C.5 | D.6 |