题目内容
点P是曲线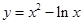 上任意一点,则点P到直线
上任意一点,则点P到直线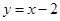 的距离的最小值是
的距离的最小值是
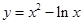 上任意一点,则点P到直线
上任意一点,则点P到直线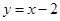 的距离的最小值是
的距离的最小值是 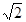
试题分析:解:设P(x,y),则y′=2x-
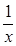 (x>0)
(x>0)令2x-
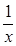 =1,则(x-1)(2x+1)=0,
=1,则(x-1)(2x+1)=0,∵x>0,∴x=1
∴y=1,即平行于直线y=x+2且与曲线y=x2-lnx相切的切点坐标为(1,1),由点到直线的距离公式可得d=
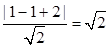 ,故答案为:
,故答案为: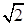 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
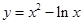 上任意一点,则点P到直线
上任意一点,则点P到直线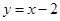 的距离的最小值是
的距离的最小值是 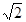
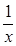 (x>0)
(x>0)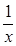 =1,则(x-1)(2x+1)=0,
=1,则(x-1)(2x+1)=0,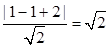 ,故答案为:
,故答案为: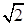 .
.
 名校课堂系列答案
名校课堂系列答案