题目内容
若一个n面体中有m个面是直角三角形,则称这个n面体的“直度”为
,已知长方体ABCD-A1B1C1D1,那么四面体A-A1B1C1的“直度”是( )
| m |
| n |
分析:根据正方体的几何特征,可由AA1⊥平面A1B1C1,判断出△AA1B1,△AA1C1是否为直角三角形;又由B1C1⊥平面AA1B1,可判断出△AB1C1,△A1B1C1是否为直角三角形,进而根据“直度”的定义,得到答案.
解答: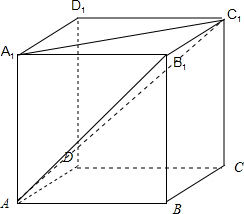 解:由题意知四面体A-A1B1C1中有4个面,
解:由题意知四面体A-A1B1C1中有4个面,
由于AA1⊥平面A1B1C1,故△AA1B1,△AA1C1为直角三角形
又由B1C1⊥平面AA1B1,故△AB1C1,△A1B1C1也为直角三角形
即直角三角形有△A1B1C1,△AA1B1,△AA1C1,△AB1C1,4个,
则四面体A1-ABC的直度为
=1.
故选D
 解:由题意知四面体A-A1B1C1中有4个面,
解:由题意知四面体A-A1B1C1中有4个面,由于AA1⊥平面A1B1C1,故△AA1B1,△AA1C1为直角三角形
又由B1C1⊥平面AA1B1,故△AB1C1,△A1B1C1也为直角三角形
即直角三角形有△A1B1C1,△AA1B1,△AA1C1,△AB1C1,4个,
则四面体A1-ABC的直度为
| 4 |
| 4 |
故选D
点评:本题考查空间直线与平面的位置关系,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
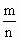 ,已知长方体
,已知长方体 ,那么四面体
,那么四面体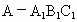 的直度是
的直度是
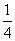



 ,已知长方体ABCD-A1B1C1D1,那么四面体A-A1B1C1的“直度”是( )
,已知长方体ABCD-A1B1C1D1,那么四面体A-A1B1C1的“直度”是( )

