题目内容
1．判断函数f（x）=$\sqrt{x+a}$（a≥0）在区间[-a，+∞）上的单调性．分析 求导数f′（x），判断其符号，从而得出f（x）在[-a，+∞）上的单调性．
解答 解：f′（x）=$\frac{1}{2\sqrt{x+a}}＞0$；
∴f（x）在[-a，+∞）上单调递增．
点评 考查根据函数导数符号判断函数单调性的方法，也可根据单调性的定义判断．
练习册系列答案
名校课堂系列答案
相关题目
2．化简（1-a）$\root{4}{\frac{1}{（a-1）^{3}}}$的结果是（ ）
| A． | $\root{4}{a-1}$ | B． | -$\root{4}{a-1}$ | C． | $\root{4}{1-a}$ | D． | -$\root{4}{1-a}$ |
9．点P坐标为（sinα-cosα，sinα+cosα），当α∈（0，2π）时，P在第二象限，则α取值范围为（ ）
| A． | （-$\frac{π}{4}$，$\frac{π}{4}$） | B． | （0，$\frac{π}{4}$）∪（$\frac{7π}{4}$，2π） | C． | （0，$\frac{π}{4}$）∪（$\frac{5π}{4}$，$\frac{7π}{4}$） | D． | （$\frac{π}{4}$，$\frac{3π}{4}$） |
6．
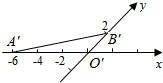如图，△O′A′B′是水平放置的△OAB的直观图，则△OAB的面积是（ ）
如图，△O′A′B′是水平放置的△OAB的直观图，则△OAB的面积是（ ）| A． | 6 | B． | 3$\sqrt{2}$ | C． | 6$\sqrt{2}$ | D． | 12 |