题目内容
设函数 是定义在
是定义在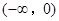 上的可导函数,其导函数为
上的可导函数,其导函数为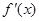 ,且有
,且有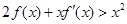 ,则不等式
,则不等式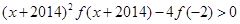 的解集为( )
的解集为( )
A.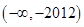 | B.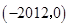 | C.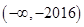 | D.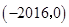 |
C
解析试题分析:由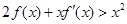 ,
,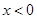 得:
得: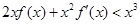 ,即
,即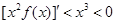 ,令
,令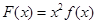 ,则当
,则当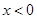 时,
时,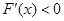 ,即
,即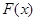 在
在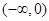 是减函数,
是减函数,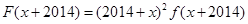 ,
,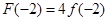 ,
,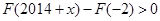 ,
,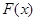 在
在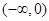 是减函数,所以由
是减函数,所以由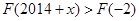 得,
得,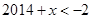 ,即
,即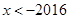 ,故选
,故选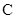
考点:1求导;2用导数研究函数的单调性。

练习册系列答案
相关题目
设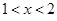 ,则
,则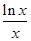 、
、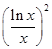 、
、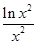 的大小关系是( )
的大小关系是( )
A. | B.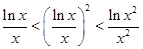 |
C.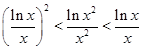 | D.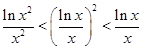 |
函数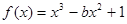 有且仅有两个不同的零点,则
有且仅有两个不同的零点,则 的值为( )
的值为( )
A.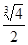 | B.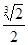 | C.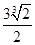 | D.不确定 |
若函数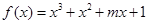 是R上的单调函数,则实数m的取值范围是( )
是R上的单调函数,则实数m的取值范围是( )
A.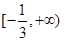 | B.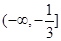 | C.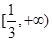 | D.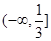  |
函数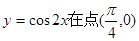 处的切线方程是
处的切线方程是
A.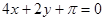 | B.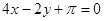 | C.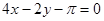 | D.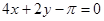 |
曲线 与
与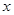 轴以及直线
轴以及直线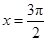 所围图形的面积为( )
所围图形的面积为( )
A.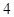 | B.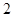 | C.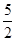 | D. |
曲线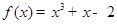 在
在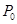 处的切线平行于直线
处的切线平行于直线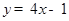 ,则
,则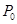 点的坐标为( )
点的坐标为( )
A.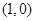 | B.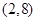 |
C.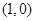 和 和 | D.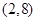 和 和 |
某公司生产一种产品,固定成本为20000元,每生产一单位的产品,成本增加100元,若总收入R与年产量x的关系是 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )
| A.150 |
| B.200 |
| C.250 |
| D.300 |
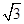 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )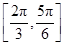
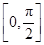 ∪
∪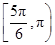
 ∪
∪