题目内容
(本小题满分12分) 已知![]() 为坐标原点,点
为坐标原点,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上运动,且
轴上运动,且![]() ,动点
,动点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,定点
,定点![]() ,直线
,直线![]() 交曲线
交曲线![]() 于另外一点
于另外一点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
解:(1)设![]() ,则
,则![]()
∵![]() ,∴
,∴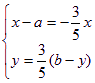 ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]()
∴曲线![]() 的方程为
的方程为![]()
(2)由(1)可知,![]() (4,0)为椭圆
(4,0)为椭圆![]() 的右焦点,设直线
的右焦点,设直线![]() 方程为
方程为
![]() ,由
,由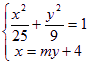 消去
消去![]() 得,
得,![]() ,
,
∴![]()
∴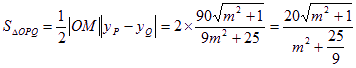
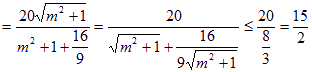 ,
,
当![]() ,即
,即![]() 时取得最大值,
时取得最大值,
此时直线方程为![]() .
.
解析:
本小题主要考查直线、椭圆等平面解析几何的基础知识,考查轨迹的求法以及综合解题能力。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目