题目内容
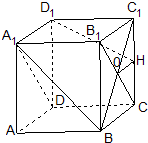 如图,在棱长为2的正方体ABCD-A1B1C1D1中,BC1∩B1C=O,H点为点O在平面D1DCC1内的正投影.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,BC1∩B1C=O,H点为点O在平面D1DCC1内的正投影.(1)求以A为顶点,四边形D1DCH为底面的四棱锥的体积;
(2)求证:BC1⊥平面A1B1CD;
(3)求直线A1B和平面A1B1CD所成的角.
分析:1)由正方体的性质可得H为CC1的中点,从而可得CH=HC1=1,由已知容易证明AD⊥平面D1DCC1,分别求出四边形D1DCH的面积及四棱锥的高CD
(2)由四边形BCC1B1是正方形可证,BC1⊥B1C,然后可证A1B1⊥BC1,根据线面垂直的平判定定理可证
(3)由(1)知BC1⊥平面A1B1CD,O为垂足,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.在RtBA1O中易求角∠BA1O
(2)由四边形BCC1B1是正方形可证,BC1⊥B1C,然后可证A1B1⊥BC1,根据线面垂直的平判定定理可证
(3)由(1)知BC1⊥平面A1B1CD,O为垂足,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.在RtBA1O中易求角∠BA1O
解答: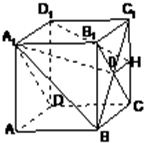 解:(1)如图,∵点O是正方形BCC1B1的中心∴H为CC1的中点,∴CH=HC1=1
解:(1)如图,∵点O是正方形BCC1B1的中心∴H为CC1的中点,∴CH=HC1=1
∴SD1DCH=
×(DD1+CH)×CD=
×(2+1)×2=3∵AD⊥DC,AD⊥DD1,CD∩DD1=D∴AD⊥平面D1DCC1,
故所求四棱锥体积为VA-D1DCH=
×SD1DCH×AD
=
×3×2=2.
(2)由题意四边形BCC1B1是正方形,∴BC1⊥B1C∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1∴A1B1⊥平面BCC1B1BC1?平面BCC1B1∴A1B1⊥BC1.(8分)
又∵B1C∩A1B1=B1,B1C?平面A1B1CD,A1B1?平面A1B1CD∴BC1⊥平面A1B1CD.
(3)如图,连A1O,由(1)知BC1⊥平面A1B1CD,O为
垂足,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.
在Rt△A1BO中,A1B=2
,BO=
,
所以∴sin∠BA1O=
=
∴∠BA1O=30°.
因此,直线A1B与平面A1B1CD所成的角为300.
 解:(1)如图,∵点O是正方形BCC1B1的中心∴H为CC1的中点,∴CH=HC1=1
解:(1)如图,∵点O是正方形BCC1B1的中心∴H为CC1的中点,∴CH=HC1=1∴SD1DCH=
| 1 |
| 2 |
| 1 |
| 2 |
故所求四棱锥体积为VA-D1DCH=
| 1 |
| 3 |
=
| 1 |
| 3 |
(2)由题意四边形BCC1B1是正方形,∴BC1⊥B1C∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1∴A1B1⊥平面BCC1B1BC1?平面BCC1B1∴A1B1⊥BC1.(8分)
又∵B1C∩A1B1=B1,B1C?平面A1B1CD,A1B1?平面A1B1CD∴BC1⊥平面A1B1CD.
(3)如图,连A1O,由(1)知BC1⊥平面A1B1CD,O为
垂足,所以A1O为斜线A1B在平面A1B1CD内的射影,∠BA1O为A1B与平面A1B1CD所成的角.
在Rt△A1BO中,A1B=2
| 2 |
| 2 |
所以∴sin∠BA1O=
| BO |
| A1B |
| 1 |
| 2 |
因此,直线A1B与平面A1B1CD所成的角为300.
点评:棱锥体积的求解的关键是需要找的与已知平面垂直的直线即所求棱锥的高,线面角的求解的关键是作出与已知平面垂直的直线,进而找到线面角,在直角三角形中求出所求的角.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )






