题目内容
14.已知数列{an}的前n项为Sn,a1=1,S10=100,且对任意正整数n,均有Sn=$\frac{n(a_n+1)}{2}$.(1)求证{an}是等差数列,并求an;
(2)数列{bn}满足bn=$\frac{1}{\sqrt{{S}_{n}}}$,记{bn}的前n项和为Tn,求证Tn>ln(n+1).
分析 (1)由Sn=$\frac{n(a_n+1)}{2}$,即2Sn=nan+n,当n≥2时,2Sn-1=(n-1)an-1+(n-1),可得2an=nan-(n-1)an-1+1,同理可得2an+1=(n+1)an+1-nan+1,可得2an=an-1+an+1,再利用等差数列的通项公式即可得出;
(2)由(1)可得:Sn=$\frac{n(a_n+1)}{2}$=n2,可得bn=$\frac{1}{\sqrt{{S}_{n}}}$=$\frac{1}{n}$,因此{bn}的前n项和为Tn=1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$.首先证明ln(1+x)<x,x>0,利用导数研究其单调性即可得出.再利用数学归纳法证明:Tn>ln(n+1)即可.
解答 证明:(1)∵Sn=$\frac{n(a_n+1)}{2}$,即2Sn=nan+n,
当n≥2时,2Sn-1=(n-1)an-1+(n-1),
∴2an=nan-(n-1)an-1+1,同理可得2an+1=(n+1)an+1-nan+1,
∴2an=an-1+an+1,
∴{an}是等差数列,设公差为d,
∵a1=1,S10=100,
∴$\frac{10(1+{a}_{10})}{2}$=100,解得a10=19,
∴1+9d=19,解得d=2,
∴an=1+2(n-1)=2n-1.
(2)由(1)可得:Sn=$\frac{n(a_n+1)}{2}$=n2,
∴bn=$\frac{1}{\sqrt{{S}_{n}}}$=$\frac{1}{n}$,
∴{bn}的前n项和为Tn=1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$,
首先证明ln(1+x)<x,x>0,
令f(x)=ln(1+x)-x,f′(x)=$\frac{1}{1+x}-1$=$\frac{-x}{1+x}$<0,
∴函数f(x)在(0,+∞)上单调递减,
∴f(x)<f(0)=0,
∴ln(1+x)<x,x>0,成立.
下面利用数学归纳法证明:Tn>ln(n+1).
(i)当n=1时,1>ln2,成立;
(ii)假设当n=k时,Tk>ln(k+1),
则当n=k+1时,
${T}_{k+1}={T}_{k}+\frac{1}{k+1}$>ln(k+1)+$\frac{1}{k+1}$=ln(k+1)-ln(k+2)+$\frac{1}{k+1}$+ln(k+2)
=$\frac{1}{k+1}-ln(1+\frac{1}{k+1})$+ln(k+2)>ln(k+1+1),
因此当n=k+1时,不等式成立.
综上可得:?n∈N*,Tn>ln(n+1)成立.
点评 本题考查了递推式的应用、等差数列的通项公式及其前n项和公式、数学归纳法,考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | -7 | B. | 7 | C. | C-4 | D. | 4 |
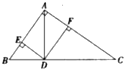 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB与E.求证
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB与E.求证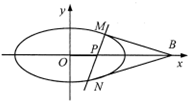 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,过点P(1,0)作斜率为k的直线l,且直线l与椭圆C交于两个不同的点M、N.
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,过点P(1,0)作斜率为k的直线l,且直线l与椭圆C交于两个不同的点M、N.