题目内容
3．在△ABC中，B=60°，面积为10$\sqrt{3}$cm2，周长为20cm，求AC的长度．分析 由三角形面积公式解得ac=40，结合周长可求得：a+c=20-b，利用余弦定理即可求得AC的长度．
解答 解：依题意得，$\frac{1}{2}acsin{60°}=10\sqrt{3}⇒ac=40$；…..（4分）
由a+b+c=20，可得：a+c=20-b，…（5分）
由余弦定理得，b2=a2+c2-2accos60°，
即b2=（a+c）2-2ac-2accos60°…（9分）
∴b2=（20-b）2-2×$40-2×40×\frac{1}{2}$，…（11分）
解锝：b=7，即AC=7…．（12分）
点评 本题主要考查了三角形面积公式，余弦定理在三角形中的应用，熟练掌握公式及定理是解题的关键，属于中档题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
14．下列函数的图象与函数y=3x的图象关于y轴对称的是（ ）
| A． | y=-3x | B． | y=-3-x | C． | $y={x^{\frac{1}{3}}}$ | D． | $y={（\frac{1}{3}）^x}$ |
15．
已知|$\overrightarrow{a}$|=2$\sqrt{2}$，|$\overrightarrow{b}$|=3，$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{4}$，如图所示，若$\overrightarrow{AB}$=5$\overrightarrow{a}$+2$\overrightarrow{b}$，$\overrightarrow{AC}$=$\overrightarrow{a}$-3$\overrightarrow{b}$，且D为BC中点，则$\overrightarrow{AD}$的长度为（ ）
已知|$\overrightarrow{a}$|=2$\sqrt{2}$，|$\overrightarrow{b}$|=3，$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{4}$，如图所示，若$\overrightarrow{AB}$=5$\overrightarrow{a}$+2$\overrightarrow{b}$，$\overrightarrow{AC}$=$\overrightarrow{a}$-3$\overrightarrow{b}$，且D为BC中点，则$\overrightarrow{AD}$的长度为（ ）| A． | $\frac{15}{2}$ | B． | $\frac{\sqrt{15}}{2}$ | C． | 7 | D． | 8 |
12．已知全集U={1，2，4，6，8，10}，集合A={2，8}，B={2，4，10}，则∁U（A∩B）=（ ）
| A． | {2，4，8，10} | B． | {1，6} | C． | {1，4，6，8，10} | D． | {2，6} |
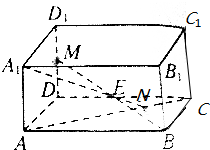已知长方体ABCD-A1B1C1D1中，M为DD1的中点，N在AC上，且AN：NC=2：1，E为BM的中点．求证：A1，E，N三点共线．