题目内容
解答题:应写出文字说明,演算步骤或证明过程
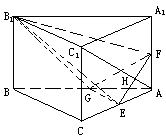
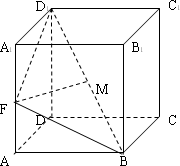
如下图,在直三棱柱ABC—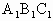 中,AC=BC=
中,AC=BC=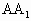 =2,∠ACB=
=2,∠ACB=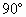 ,E、F、G分别为AC、
,E、F、G分别为AC、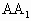 、AB的中点,
、AB的中点,
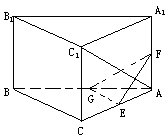
(Ⅰ)求证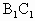 ∥平面EFG;
∥平面EFG;
(Ⅱ)求FG与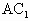 所成的角;
所成的角;
(Ⅲ)求证:FG⊥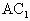 ;
;
(Ⅳ)求三棱锥 —EFG的体积.
—EFG的体积.
答案:
解析:
解析:
|
(Ⅰ)证明在直三棱柱ABC- 又已知E、G分别为AC、AB的中点,故EG为△ABC的中位线. ∴BC∥EG. ∴ 又∵EG ∴ (Ⅱ)(Ⅲ)直三棱柱ABC— 而EG ∴EG⊥ 又已知∠ACB= ∵EG∥BC, 故EG⊥AC. 由于AC∩ ∴EG⊥侧面 ∵ ∴EG⊥ 又已知AC= ∵E、F分别为AC、 据平面几何知识,得EF⊥ 由于EG∩EF=E,EGÌ 平面EFG,EFÌ 平面EFG, ∴ ∵FGÌ 平面EFG, ∴ 故 (Ⅳ)∵ ∴ 又∵ ∴
|

练习册系列答案
相关题目
| |||||||||||||||
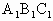 中,有
中,有 ∥BC.
∥BC.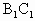 ∥EG.
∥EG. 平面EFG,
平面EFG,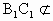 平面EFG,
平面EFG,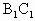 ∥平面EFG.
∥平面EFG.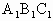 的棱
的棱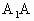 ⊥底面ABC,
⊥底面ABC, 底面ABC,
底面ABC,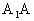 ,
,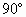 ,即BC⊥AC,
,即BC⊥AC, =A,AC
=A,AC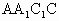 ,
,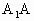 侧面
侧面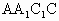 .
.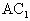 Ì
侧面
Ì
侧面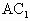 .
. =2,可有侧面
=2,可有侧面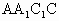 为正方形.
为正方形.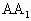 的中点,
的中点,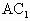 .
.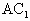 ⊥平面EFG,
⊥平面EFG,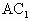 ⊥FG.
⊥FG.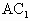 与FG所成的角是
与FG所成的角是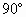 .
.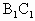 ∥平面EFG,
∥平面EFG,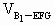 =
=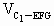 .
.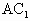 ⊥平面EFG,设
⊥平面EFG,设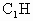 为三棱锥
为三棱锥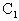 —EFG的高,
—EFG的高,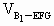 =
=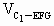 =
=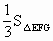 ·
·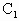 H
H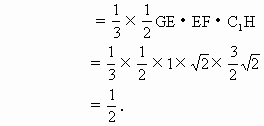
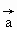 |=1,|
|=1,|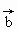 |=2,
|=2,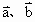 ;
;

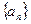 中,
中,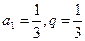 ,
,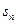 为数列
为数列 项的和,证明:
项的和,证明:
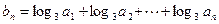 ,求数列
,求数列 的通项公式;
的通项公式;