题目内容
16.$f(x)=\left\{\begin{array}{l}1,\;\;\;\;\;x>0\\ 0,\;\;\;\;\;x=0\\-1,\;\;x<0,\;\;\end{array}\right.$g(x)=x2f(x-1),(1)求g(x)的解析式;
(2)画出函数g(x)的图象,并写出其单调区间.
分析 (1)由分段函数可写出$g(x)=\left\{\begin{array}{l}{x^2},\;\;\;\;\;x>1\\ 0,\;\;\;\;\;x=1\\-{x^2},\;\;x<1,\;\;\end{array}\right.$;
(2)作函数g(x)的图象,从而写出单调区间即可.
解答 解:(1)由题意得,
$g(x)=\left\{\begin{array}{l}{x^2},\;\;\;\;\;x>1\\ 0,\;\;\;\;\;x=1\\-{x^2},\;\;x<1,\;\;\end{array}\right.$;
(2)作函数g(x)的图象如下,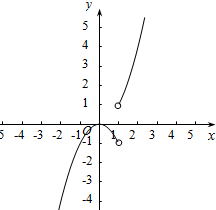 ,
,
结合图象可知,其单调增区间为(-∞,0],(1,+∞);
单调减区间[0,1).
点评 本题考查了分段函数的应用及函数的图象的作法与应用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
4.若变量x,y满足$\left\{\begin{array}{l}{x+y-3≥0}\\{x-2y-4≤0}\\{x-4y+4≥0}\end{array}\right.$,则z=x-y的最大值为8.
8.△ABC中,sinA:sinB:sinC=3:5:7,则△ABC中最大角的度数是( )
| A. | 150° | B. | 120° | C. | 90° | D. | 135° |
5.连续抛掷两次骰子,所得的点数之和能被3整除的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{11}{36}$ | D. | $\frac{5}{6}$ |
6.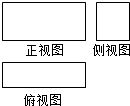 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |