题目内容
已知关于x的方程(1-a)x2+(a+2)x-4=0,a∈R,求:(1)方程有两个正根的充要条件;
(2)方程至少有一个正根的充要条件.
解析:先求出方程有两个实根的充要条件,再讨论x2的系数及运用根与系数的关系分别求出要求的充要条件.
解:(1)方程(1-a)x2+(a+2)x-4=0有两个实根的充要条件是![]()
即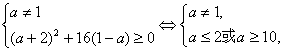 即a≥10或a≤2且a≠1.
即a≥10或a≤2且a≠1.
设此时方程的两实根为x1、x2,有两个正根的充要条件是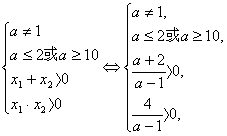
即1<a≤2或a≥10是方程有两个正根的充要条件.
(2)由(1)知当1<a≤2或a≥10时方程有两个正根,当a=1时,方程化为3x-4=0,有一正根![]() ,又方程有一正根一负根的充要条件是a<1,故方程至少有一个正根的充要条件是a≤2或a≥10.
,又方程有一正根一负根的充要条件是a<1,故方程至少有一个正根的充要条件是a≤2或a≥10.
启示:处理充分、必要条件问题时,首先要分清条件与结论,要紧扣定义.

练习册系列答案
相关题目