题目内容
已知关于x的方程(1-a)x2+(a+2)x-4=0,a∈R,求:(1)方程有两个正根的充要条件;
(2)方程至少有一正根的充要条件?
方程有两个实根的充要条件是
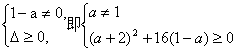
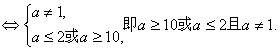 ?
?
(1)设此方程的两个实数根为x1、x2,则方程有两个正根
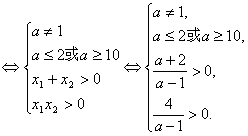
解得1<a≤2或a≥10?
∴1<a≤2或a≥10是方程有两个正根的充要条件?
(2)①由(1)可知,当a≥10或1<a≤2时,方程有两个正根;
②方程有一正根一负根的充要条件是x1x2<0![]() ,即a<1;
,即a<1;
③当a=1时,方程可化为3x-4=0,有一正根x=![]() .
.
综上①②③,可知方程(1-a)x2+(a+2)x-4=0至少有一正根的充要条件是a≤2或a≥10.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目