题目内容
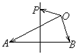 如图,O、A、B是平面上的三点,P为线段AB的中垂线上的任意一点,若|
如图,O、A、B是平面上的三点,P为线段AB的中垂线上的任意一点,若|| OA |
| OA |
| OP |
| OA |
| OB |
分析:利用线段垂直平方线上的点到线段两个端点的距离相等得到|
|=|
|;利用向量的运算法则可得
|
-
|=|
-
|,将此等式平方化简,可得
•(
-
)的值.
| BP |
| AP |
|
| OP |
| OB |
| OP |
| OA |
| OP |
| OA |
| OB |
解答:解:由线段垂直平方线上的点到线段两个端点的距离相等得到|
|=|
|,故有 |
-
|=|
-
|.
平方可得
2+
2-2
•
=
2+
2-2
•
,
把|
|=4,|
|=2 代入,化简可得 2
•(
-
)=12,即
•(
-
)=6,
故选A.
| BP |
| AB |
| OP |
| OB |
| OP |
| OA |
平方可得
| OP |
| OB |
| OP |
| OB |
| OP |
| OA |
| OP |
| OA |
把|
| OA |
| OA |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
故选A.
点评:本题考查线段垂直平方线的性质、向量的运算法则、向量模的平方等于向量的平方,关于向量的基础知识要牢记,
以免出现错误,属于中档题.
以免出现错误,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
 )
) 设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么你类比得到的结论是( )
表示截面面积,那么你类比得到的结论是( )
 B.
B.
 D.
D.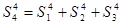
 )
)