题目内容
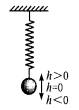
 弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置h厘米有下列关系确定h=2sin(t+
弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置h厘米有下列关系确定h=2sin(t+| π | 4 |
(1)以t为横坐标,h为纵坐标,作出这个函数在一个周期内的图象;
(2)小球在开始震动时的位置在哪里?
(3)小球的最高点和最低点与平衡位置的距离分别是多少?
(4)经过多少时间小球往复运动一次?
(5)每秒钟小球能往复振动多少次?
分析:(1)由三角函数h=sint的图象变换可得所求函数的图象;(2)把t=0代入已知函数,求得y值即可得初始位置;(3)又解析式可得振幅,即为所求;(4)求函数周期可得所求;(5)由频率的意义可得.
解答:解:(1)由题意可得h=2sin(t+
)的图象,

(2)由题意可得当t=0时,h=2sin(0+
)=
,
故小球在开始震动时的位置在(0,
),
(3)由解析式可得振幅A=2,
故小球的最高点和最低点与平衡位置的距离均为2(厘米);
(4)可得函数的周期为T=2π,故小球往复运动一次需2π,
(5)可得频率为
,即每秒钟小球能往复振动
次
| π |
| 4 |

(2)由题意可得当t=0时,h=2sin(0+
| π |
| 4 |
| 2 |
故小球在开始震动时的位置在(0,
| 2 |
(3)由解析式可得振幅A=2,
故小球的最高点和最低点与平衡位置的距离均为2(厘米);
(4)可得函数的周期为T=2π,故小球往复运动一次需2π,
(5)可得频率为
| 1 |
| 2π |
| 1 |
| 2π |
点评:本题考查三角函数的图象,及其各参数的物理意义,属中档题.

练习册系列答案
相关题目