题目内容
已知双曲线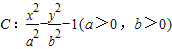 的两个焦点为
的两个焦点为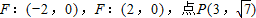
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为
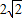 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)根据题意可得a2+b2=4,得到a和b的关系,把点(3,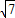 )代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.
)代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.
(2)可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,根据直线I与双曲线C相交于不同的两点E、F,进而可得k的范围,设E(x1,y1),F(x2,y2),根据韦达定理可求得x1+x2和x1x2,进而表示出|EF|和原点O到直线l的距离根据三角形OEF的面积求得k,进而可得直线方程.
解答:解:(Ⅰ):依题意,由a2+b2=4,得双曲线方程为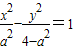 (0<a2<4),
(0<a2<4),
将点(3,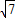 )代入上式,得
)代入上式,得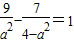 .解得a2=18(舍去)或a2=2,
.解得a2=18(舍去)或a2=2,
故所求双曲线方程为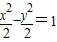 .
.
(Ⅱ):依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线I与双曲线C相交于不同的两点E、F,
∴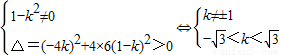
∴k∈(-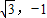 )∪(1,
)∪(1,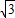 ).
).
设E(x1,y1),F(x2,y2),则由①式得x1+x2=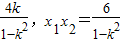 ,
,
于是,|EF|=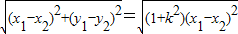
=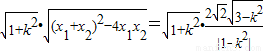
而原点O到直线l的距离d=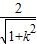 ,
,
∴S△OEF=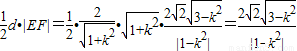 .
.
若S△OEF=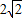 ,即
,即 ,解得k=±
,解得k=±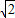 ,
,
满足②.故满足条件的直线l有两条,其方程分别为y=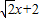 和
和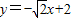 .
.
点评:本题主要考查了双曲线的方程和双曲线与直线的关系.考查了学生综合运算能力.
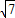 )代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.
)代入双曲线方程,求得a,进而根据a2+b2=4求得b,双曲线方程可得.(2)可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,根据直线I与双曲线C相交于不同的两点E、F,进而可得k的范围,设E(x1,y1),F(x2,y2),根据韦达定理可求得x1+x2和x1x2,进而表示出|EF|和原点O到直线l的距离根据三角形OEF的面积求得k,进而可得直线方程.
解答:解:(Ⅰ):依题意,由a2+b2=4,得双曲线方程为
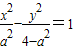 (0<a2<4),
(0<a2<4),将点(3,
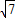 )代入上式,得
)代入上式,得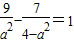 .解得a2=18(舍去)或a2=2,
.解得a2=18(舍去)或a2=2,故所求双曲线方程为
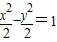 .
.(Ⅱ):依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线I与双曲线C相交于不同的两点E、F,
∴
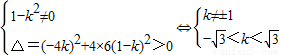
∴k∈(-
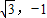 )∪(1,
)∪(1,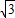 ).
).设E(x1,y1),F(x2,y2),则由①式得x1+x2=
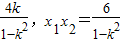 ,
,于是,|EF|=
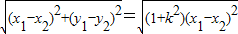
=
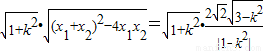
而原点O到直线l的距离d=
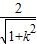 ,
,∴S△OEF=
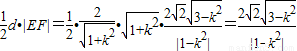 .
.若S△OEF=
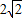 ,即
,即 ,解得k=±
,解得k=±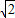 ,
,满足②.故满足条件的直线l有两条,其方程分别为y=
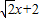 和
和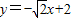 .
.点评:本题主要考查了双曲线的方程和双曲线与直线的关系.考查了学生综合运算能力.

练习册系列答案
相关题目
已知双曲线的两个焦点为F1(-
,0)、F2(
,0),P是此双曲线上的一点,且PF1⊥PF2,|PF1|•|PF2|=2,则该双曲线的方程是( )
| 5 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
已知双曲线的两个焦点是椭圆
+
=1的两个顶点,双曲线的两条准线经过椭圆的两个焦点,则此双曲线的方程是( )
| x2 |
| 100 |
| y2 |
| 64 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|