题目内容
数列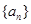 的前
的前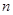 项和为
项和为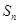 ,
,
若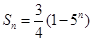 ,则
,则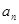 =
;
=
;
若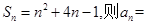 。
。
【答案】
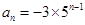
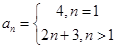
【解析】解:因为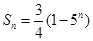 ,那么对于n令值n=1,得到首项为-3,当n
,那么对于n令值n=1,得到首项为-3,当n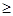 2时,得到
2时,得到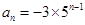 ,综上可知填写
,综上可知填写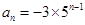
又因为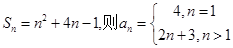

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
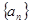 中,
中,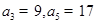 ,记数列
,记数列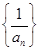 的前
的前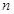 项和为
项和为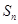 ,若
,若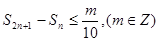 ,对任意的
,对任意的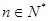 成立,则整数
成立,则整数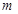 的最小值为( )
的最小值为( )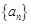 的前
的前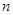 项和为
项和为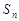 ,若对任意
,若对任意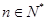 ,都有
,都有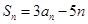 .
.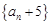 是等比数列,并求数列
是等比数列,并求数列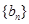 满足
满足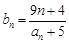 ,问是否存在
,问是否存在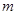 ,使得
,使得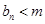 恒成立?如果存在,求出
恒成立?如果存在,求出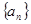 的各项都为正数,
的各项都为正数,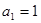 ,前
,前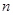 项和
项和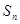 满足
满足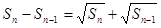 (
(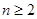 ).
).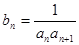 (
(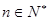 ),数列
),数列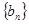 的前
的前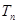 ,若
,若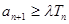 对任意正整数
对任意正整数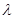 的取值范围.
的取值范围.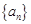 的前
的前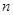 项和为
项和为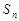 ,若对任意
,若对任意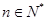 ,都有
,都有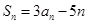 .
.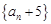 是等比数列,并求数列
是等比数列,并求数列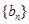 满足
满足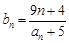 ,问是否存在
,问是否存在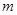 ,使得
,使得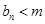 恒成立?如果存在,求出
恒成立?如果存在,求出