题目内容
已知函数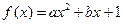
(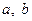 为实数,
为实数,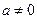 ,
,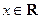 ),
),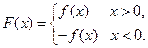
(Ⅰ)若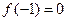 ,且函数
,且函数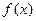 的值域为
的值域为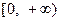 ,求
,求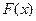 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当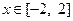 时,
时,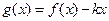 是单调函数,求实数
是单调函数,求实数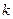
的取值范围;
(Ⅲ)设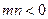 ,
,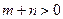 ,
,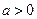 ,且函数
,且函数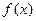 为偶函数,判断
为偶函数,判断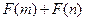 是
是
否大于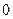 ?
?
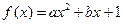
(
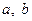 为实数,
为实数,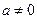 ,
,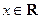 ),
),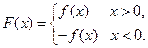
(Ⅰ)若
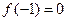 ,且函数
,且函数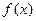 的值域为
的值域为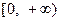 ,求
,求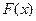 的表达式;
的表达式;(Ⅱ)在(Ⅰ)的条件下,当
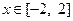 时,
时,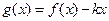 是单调函数,求实数
是单调函数,求实数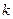
的取值范围;
(Ⅲ)设
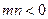 ,
,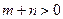 ,
,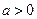 ,且函数
,且函数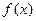 为偶函数,判断
为偶函数,判断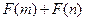 是
是否大于
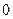 ?
?(Ⅰ)
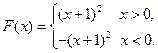
(Ⅱ)
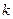 的范围是
的范围是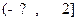 或
或 时,
时,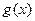 是单调函数
是单调函数(Ⅲ)
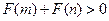
解:(Ⅰ)因为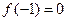 ,所以
,所以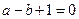 .
.
因为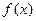 的值域为
的值域为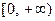 ,所以
,所以 ……………………… 2分
……………………… 2分
所以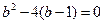 . 解得
. 解得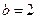 ,
,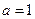 . 所以
. 所以 .
.
所以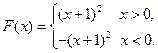 …………………………………… 4分
…………………………………… 4分
(Ⅱ)因为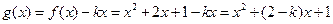
=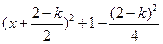 , ………………………… 6分
, ………………………… 6分
所以当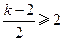 或
或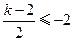 时
时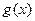 单调.
单调.
即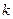 的范围是
的范围是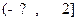 或
或 时,
时,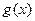 是单调函数. …………… 8分
是单调函数. …………… 8分
(Ⅲ)因为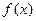 为偶函数,所以
为偶函数,所以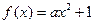 .
.
所以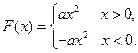 ………………………………………… 10分
………………………………………… 10分
因为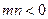 , 依条件设
, 依条件设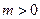 ,则
,则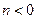 .
.
又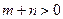 ,所以
,所以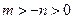 .
.
所以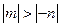 . …………………………………………………… 12分
. …………………………………………………… 12分
此时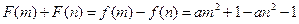
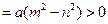 .
.
即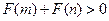 . ………………………………………………… 13分
. ………………………………………………… 13分
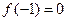 ,所以
,所以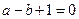 .
.因为
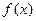 的值域为
的值域为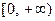 ,所以
,所以 ……………………… 2分
……………………… 2分所以
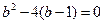 . 解得
. 解得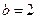 ,
,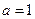 . 所以
. 所以 .
.所以
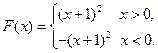 …………………………………… 4分
…………………………………… 4分(Ⅱ)因为
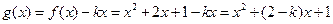
=
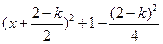 , ………………………… 6分
, ………………………… 6分所以当
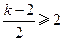 或
或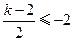 时
时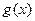 单调.
单调.即
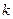 的范围是
的范围是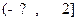 或
或 时,
时,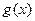 是单调函数. …………… 8分
是单调函数. …………… 8分(Ⅲ)因为
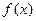 为偶函数,所以
为偶函数,所以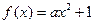 .
. 所以
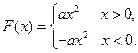 ………………………………………… 10分
………………………………………… 10分因为
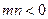 , 依条件设
, 依条件设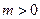 ,则
,则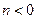 .
.又
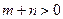 ,所以
,所以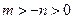 .
.所以
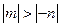 . …………………………………………………… 12分
. …………………………………………………… 12分此时
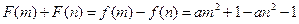
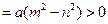 .
.即
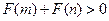 . ………………………………………………… 13分
. ………………………………………………… 13分
练习册系列答案
相关题目
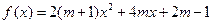
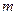 取何值时,函数的图象与
取何值时,函数的图象与 轴有两个零点;
轴有两个零点; 满足
满足 且
且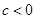 ,则含有
,则含有 零点的一个区间是( )
零点的一个区间是( )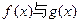 图象交于不同的两点;
图象交于不同的两点;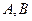 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。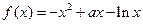 (
(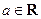 ).
).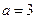 时,求函数
时,求函数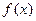 在
在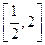 上的最大值和最小值;
上的最大值和最小值;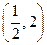 单调时,求
单调时,求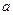 的取值范围;
的取值范围;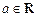 ,
,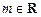 ,函数
,函数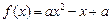 。若
。若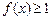 对
对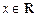 都成立,求
都成立,求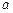 的取值范围。
的取值范围。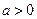 ,函数
,函数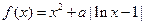 .
.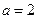 时,求函数
时,求函数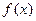 的单调增区间;
的单调增区间;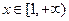 时,不等式
时,不等式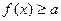 恒成立,实数
恒成立,实数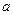 的取值范围
的取值范围 ,在使
,在使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的下确界为
的下确界为  ,则
,则