题目内容
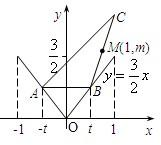 如图,函数y=
如图,函数y=| 3 |
| 2 |
| 3 |
| 2 |
(1)写出用B的横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标.
分析:(1)欲求△ABC面积S,关键是求边AB的长及相应的高,依题意,设B(t,
t),A(-t,
t)(t>0),C(x0,y0).求出△ABC中边|AB|及AB边上的高h,再利用三角形的面积公式计算即得;
(2)先对函数式进行了配方得:S=-3t2+2mt=-3(t-
)2+
,t∈(0,1].下面结合二次函数的图象与性质求解其最大值即可.
| 3 |
| 2 |
| 3 |
| 2 |
(2)先对函数式进行了配方得:S=-3t2+2mt=-3(t-
| m |
| 3 |
| m2 |
| 3 |
解答:解:(1)依题意,设B(t,
t),A(-t,
t)(t>0),C(x0,y0).
∵M是BC的中点,∴
=1,
=m,∴x0=2-t,y0=2m-
t.
在△ABC中,|AB|=2t,AB边上的高h=y0-
t=2m-3t.
∴S=
|AB|•h=
•2t•(2m-3t)=-3t2+2mt,t∈(0,1].
(2)S=-3t2+2mt=-3(t-
)2+
,t∈(0,1].若
,
即
<m≤3.当t=
时,Smax=
,相应的C点坐标是(2-
,
m).
若
>1,即m>3时,S=f(t)在区间(0,1]上是增函数,
∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-
).
| 3 |
| 2 |
| 3 |
| 2 |
∵M是BC的中点,∴
| t+x0 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
在△ABC中,|AB|=2t,AB边上的高h=y0-
| 3 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)S=-3t2+2mt=-3(t-
| m |
| 3 |
| m2 |
| 3 |
|
即
| 3 |
| 2 |
| m |
| 3 |
| m2 |
| 3 |
| m |
| 3 |
| 3 |
| 2 |
若
| m |
| 3 |
∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-
| 3 |
| 2 |
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数的知识解决实际问题的能力.属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3, 函数y=f(x)在定义域
函数y=f(x)在定义域 如图,函数
如图,函数